题目内容
如图所示，一根质量为
的金属棒
水平放置在两根竖直的光滑平行金属导轨上，并始终与导轨保持良好接触，导轨间距为L，导轨下端接一阻值为
的电阻，其余电阻不计。在空间内有垂直于导轨平面的磁场，磁感应强度大小只随竖直方向
变化，变化规律
，
为大于零的常数。质量为
的物体静止在倾角θ=30°的光滑斜面上，并通过轻质光滑定滑轮和绝缘细绳与金属相连接。当金属棒沿轴方向从
位置由静止开始向上运动
时，加速度恰好为0。不计空气阻力，斜面和磁场区域足够大，重力加速度为
。求：
（1）金属棒上升时的速度；
（2）金属棒上升的过程中，电阻R上产生的热量；
（3）金属棒上升的过程中，通过金属棒横截面的电量。
 |
（1）当金属棒的加速度为零时，
Mgsin30°=F+mg 2分
F=BIL=KhIL 1分
1分
解以上方程得
1分
（2）设产生的焦耳热为Q，由动能定理，有
3分
得：
2分
（3）
1分
1分
1分
2分
解得：
1分
如图所示，一根质量为m的金属棒AC用软线悬挂在磁感强度为B的匀强磁场中，通入A→C方向的电流时，悬线张力不为零，欲使悬线张力为零，可以采用的办法是（ ）
如图所示，一根质量为m的金属棒AC，用软线悬挂在磁感应强度为B的匀强磁场中，电流方向由A→C，此时悬线张力不为零，欲使悬线张力为零，必须（ ）
如图所示，一根质量为m、长为L的均匀长方体木料放在水平桌面上，木料与桌面间的滑动摩擦力大小为重力的μ倍．现用一水平力F推木料，当木料经过图示位置时，桌面对它的滑动摩擦力大小为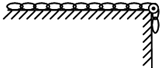
如图所示，一根质量为 m、长为L的匀质链条，一端位于光滑的水平桌面上，另一端少许下垂于桌子边缘，并绕过光滑的定滑轮从静止开始下滑．设桌面足够高，则链条在下滑的过程中，对滑轮产生的最大压力是（ ）
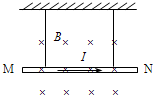如图所示，一根质量为m的金属棒MN用细线悬挂在磁感应强度为B的匀强磁场中，通入沿M→N方向的电流时，悬线对金属棒的拉力不为零．若要使悬线对棒的拉力为零，可以采用的办法是（ ）