题目内容
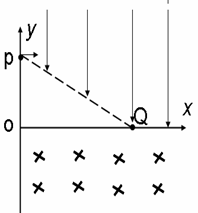
(2013河南平顶山期末)如图所示，在xoy平面内的第一象限有一以PQ为边界、沿y轴负向的匀强电场E，在第四象限有垂直于xoy平面的匀强磁场B。某时有质量和电荷量均为m、q的正粒子a、b同时从P点以垂直于y轴的速度进入电场，速度大小分别为v0、2v0，b粒子从Q点进入磁场。 P、Q的坐标分别是（0，l）、（2l，0）。不计重力，不考虑粒子间的相互作用和可能发生的碰撞。
（1）求电场强度E的大小。
（2）调节磁感应强度B使粒子b首次在磁场中运动的时间跟在电场中运动的时间相等，设这一时间为TO，求TO及对应的磁感应强度B。
（3）在保持上述磁感应强度不变的情况下，求当a、b中的一个粒子第二次到达x轴时另一粒子的y坐标，最终表达式的系数保留一位小数即可。
（半角公式
)
解析：（18分）
（1） 以b为对象可知，
（2分）
（2分）
且y=l，x=2l
解得：
（2分）
（3）设粒子离开电场时速度方向与x轴夹角为为
：
即与x轴夹角为为450（1分）
a粒子在电场中运动时间：
a粒子离开电场运动到x轴的时间：
a粒子从P点运动到x轴的时间：
（1分）
故：a粒子比b粒子晚进入磁场的时间：
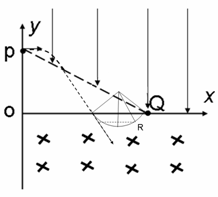
b粒子离开磁场到达x轴时，a在磁场中运动了
，即到达图中的R点
a进入磁场的速度
（1分）
由
得：（1分）
（1分）
R的y坐标为：y=ra(cos45°-cos22.5°)=-0.2l（1分）
练习册系列答案
相关题目
也被比作“刀尖上的舞蹈”，着舰跑道长度只有陆地机场跑道的1/10，尽管航母甲板总长有300多米，但能够提供舰载机起飞、着舰使用的距离只有百米左右，舰载机要在浮动的航母甲板上钩住阻拦索，难度非常大。中国舰载战机“歼-15”成功在“辽宁舰”航空母舰上完成起降着舰，为航母战斗力的组建迈出重要一步。某同学为了研究“歼-15”舰载机的起飞过程，把其运动过程简化如下：其轨道由长为L=1.5m的水平轨道AB和圆弧轨道BC相接，圆弧轨道半径R=2m，圆心在B点正上方O处，弧BC所对的圆心角为θ=370，具有动力装置的玩具小车质量为m=1kg，从A点开始以恒定功率P=10W由静止开始启动，运动至B点时撤去动力，小车沿圆弧轨道继续运动至C点时对轨道的压力为FN=26N，整个过程所受阻力恒为f=0.1mg（取g=10m/s2，sin370=0.6,cos370=0.8）. 求：
)一束单色光由左侧射入盛有清水的薄壁圆柱，图2为过轴线的截面图，调整入射角α，光线恰好在和空气的界面上发生全反射，已知水的折射率为4/3，求sinα的值。
