题目内容
14. 如图所示,一个质量为m、带电量为q的微粒,从a点以初速度v0竖直向上射入图示的匀强电场中.粒子通过b点时的速度为v0,方向水平向右.求电场强度E和a、b两点间的电势差U.
如图所示,一个质量为m、带电量为q的微粒,从a点以初速度v0竖直向上射入图示的匀强电场中.粒子通过b点时的速度为v0,方向水平向右.求电场强度E和a、b两点间的电势差U.
分析 采用运动的分解法研究:水平方向小球只受电场力做匀加速直线运动,根据动能定理求出a、b两点的电势差.由动量定理求电场强度.
解答 解:小球水平方向只受电场力做匀加速直线运动,根据动能定理得:
qUab=$\frac{1}{2}m{v}_{0}^{2}$
得:a、b两点的电势差为:Uab=$\frac{m{v}_{0}^{2}}{2q}$.
水平方向上运动的时间与竖直方向上运动的时间是相等的,设运动的时间是t,则根据动量定理得:
竖直方向有-mgt=0-mv0
水平方向有 qEt=mv0-0
所以:qE=mg
得E=$\frac{mg}{q}$
答:电场强度E是$\frac{mg}{q}$,a、b两点间的电势差U是$\frac{m{v}_{0}^{2}}{2q}$.
点评 本题考查灵活选择处理曲线运动的能力.小球在水平和竖直两个方向受到的都是恒力,运用运动的合成与分解法研究是常用的思路.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.两颗行星各有一颗卫星绕其表面运行,已知两卫星的周期之比为1:2,两行星的半径之比为2:1,则下列结论正确的是( )
| A. | 两行星的质量之比为16:1 | |
| B. | 两行星的密度之比为1:4 | |
| C. | 两行星表面处重力加速度之比为8:1 | |
| D. | 两卫星的速率之比为4:1 |
2.在静电场中,将一个电子由a点移到b点,电场力做功5eV,下面判断中正确的是( )
| A. | 电场强度的方向一定由a指向b | B. | 电场强度的方向一定由b指向a | ||
| C. | 电子的电势能减少了5eV | D. | a、b两点电势差Uab=5V |
9.下列说法正确的是( )
| A. | 物体所受的力越大,它的惯性越大 | |
| B. | 速度大的物体不容易停下,是因为物体速度越大,惯性越大 | |
| C. | 宇宙飞船内的物体处于完全失重状态,因此飞船内的物体不存在惯性 | |
| D. | 对于任何物体,在受到相同的作用力时,决定它们运动状态变化难易程度的惟一因素就是它们的质量 |
19. 如图所示,范围足够大、磁感应强度为B的匀强磁场垂直于xoy平面向里,两质量相等的粒子带等量异种电荷,它们从x轴上关于O点对称的两点同时由静止释放,运动过程中未发生碰撞,不计粒子所受的重力则( )
如图所示,范围足够大、磁感应强度为B的匀强磁场垂直于xoy平面向里,两质量相等的粒子带等量异种电荷,它们从x轴上关于O点对称的两点同时由静止释放,运动过程中未发生碰撞,不计粒子所受的重力则( )
 如图所示,范围足够大、磁感应强度为B的匀强磁场垂直于xoy平面向里,两质量相等的粒子带等量异种电荷,它们从x轴上关于O点对称的两点同时由静止释放,运动过程中未发生碰撞,不计粒子所受的重力则( )
如图所示,范围足够大、磁感应强度为B的匀强磁场垂直于xoy平面向里,两质量相等的粒子带等量异种电荷,它们从x轴上关于O点对称的两点同时由静止释放,运动过程中未发生碰撞,不计粒子所受的重力则( )| A. | 两粒子沿x轴做直线运动 | |
| B. | 运动过程中,若两粒子间的距离等于初始位置间的距离时,它们的速度均为零 | |
| C. | 若减小磁感应强度,再从原处同时由静止释放两粒子,它们可能会发生碰撞 | |
| D. | 运动过程中,两粒子间的距离最小时,它们的速度沿y轴方向的分量vy最小 |
6. 如图所示,一理想变压器原、副线圈的匝数比为n1:n2=10:1,原线圈通过一理想电流表A接在u=200$\sqrt{2}$sin100πt(V)的正弦交流电源上,一个二极管D和阻值为R的负载电阻串联后接到副线圈的两端,理想电压表V和电阻R并联.假设该二极管D的正向电阻为零,反向电阻为无穷大,则( )
如图所示,一理想变压器原、副线圈的匝数比为n1:n2=10:1,原线圈通过一理想电流表A接在u=200$\sqrt{2}$sin100πt(V)的正弦交流电源上,一个二极管D和阻值为R的负载电阻串联后接到副线圈的两端,理想电压表V和电阻R并联.假设该二极管D的正向电阻为零,反向电阻为无穷大,则( )
 如图所示,一理想变压器原、副线圈的匝数比为n1:n2=10:1,原线圈通过一理想电流表A接在u=200$\sqrt{2}$sin100πt(V)的正弦交流电源上,一个二极管D和阻值为R的负载电阻串联后接到副线圈的两端,理想电压表V和电阻R并联.假设该二极管D的正向电阻为零,反向电阻为无穷大,则( )
如图所示,一理想变压器原、副线圈的匝数比为n1:n2=10:1,原线圈通过一理想电流表A接在u=200$\sqrt{2}$sin100πt(V)的正弦交流电源上,一个二极管D和阻值为R的负载电阻串联后接到副线圈的两端,理想电压表V和电阻R并联.假设该二极管D的正向电阻为零,反向电阻为无穷大,则( )| A. | 交流电压表示数为20V | |
| B. | 交流电流表示数为1.41A | |
| C. | 减小负载电阻的阻值R,电流表的读数变小 | |
| D. | 将二极管短路,电流表的读数加倍 |
3.关于原子核的衰变、聚变和裂变,下列表述正确的是( )
| A. | 半衰期越短,衰变越慢 | |
| B. | 核聚变和核裂变过程都有质量亏损 | |
| C. | ${\;}_{90}^{234}$Th经过一次α衰变后变成${\;}_{91}^{234}$Pb | |
| D. | 原子核的半衰期与环境的温度、压强无关 |
4.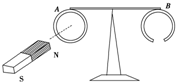 如图所示,A、B都是很轻的铝环,分别吊在绝缘细杆的两端,杆可绕竖直轴在水平面内转动,环A是闭合的,环B是断开的.若用磁铁分别靠近这两个圆环,则下面说法正确的是( )
如图所示,A、B都是很轻的铝环,分别吊在绝缘细杆的两端,杆可绕竖直轴在水平面内转动,环A是闭合的,环B是断开的.若用磁铁分别靠近这两个圆环,则下面说法正确的是( )
 如图所示,A、B都是很轻的铝环,分别吊在绝缘细杆的两端,杆可绕竖直轴在水平面内转动,环A是闭合的,环B是断开的.若用磁铁分别靠近这两个圆环,则下面说法正确的是( )
如图所示,A、B都是很轻的铝环,分别吊在绝缘细杆的两端,杆可绕竖直轴在水平面内转动,环A是闭合的,环B是断开的.若用磁铁分别靠近这两个圆环,则下面说法正确的是( )| A. | 图中磁铁N极接近A环时,A环的磁通量增加,A环被排斥 | |
| B. | 图中磁铁s极远离A环时,A环的磁通量减少,A环被排斥 | |
| C. | 图中磁铁N极接近B环时,B环的磁通量增加,B环被吸引 | |
| D. | 图中磁铁s极远离B环时,B环的磁通量减少,B环被吸引 |