题目内容
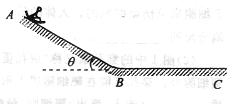
在海滨游乐园里有一种滑沙的游乐活动．如图所示，人坐在滑板上从斜坡的高处A点由静止开始滑下，滑到斜坡底部B点后沿水平滑道再滑行一段距离到C点停下来．斜坡滑道与水平滑道间是平滑连接的，滑板与两滑道间的动摩擦因数均为μ=0.50，不计空气阻力，重力加速度g=10m/s2．斜坡倾角θ=37°，人和滑板的总质量m=60kg．（1）求人在斜坡上下滑的加速度大小
（2）若斜面AB长L=60m，则人在水平滑道上滑行的距离是多少？
（3）若由于受到场地限制，A点到C点的水平距离为S=50m，为确保人身安全，你认为在设计斜坡滑道时，对高度应有怎样的要求？（sin37°=0.6，cos37°=0.8）
分析：（1）对人和滑板进行受力分析，根据牛顿第二定律求出下滑的加速度．
（2）根据匀变速直线运动的速度位移公式求出人滑到底端的速度，根据牛顿第二定律求出人在水平滑道上的加速度，从而求出在水平滑道上滑行的距离．
（3）抓住AC的水平距离不超过50m，根据匀变速直线运动公式求出高度的范围．
（2）根据匀变速直线运动的速度位移公式求出人滑到底端的速度，根据牛顿第二定律求出人在水平滑道上的加速度，从而求出在水平滑道上滑行的距离．
（3）抓住AC的水平距离不超过50m，根据匀变速直线运动公式求出高度的范围．
解答：解：（1）在斜坡上下滑时，人及滑板受力如图所示，由牛顿第二定律得：
mgsin37°-μmgcos37°=ma
解得：a=gsin37°-μgcos37°=2m/s2．
（2）设人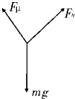
从斜坡滑道B点的速度为v，由运动学公式得：2as=v2
在水平滑道上做加速运动，加速度：a1=μg=5m/s
设在水平滑道上滑行的距离为S1，由运动学公式得：2a1s1=v2
由以上各式联立解得：S1=24m
（3）设斜坡倾角为θ，斜坡的最大高度为h，滑到底端时的速度为v，则：
v2=2a
沿BC前进时的加速度：a′=μg，
沿BC滑行的距离：L=
．
为确保安全要求，则：L+hcotθ≤S．
联立解得：h≤25m．
答：（1）人在斜坡上下滑的加速度大小为2m/s2．
（2）人在水平滑道上滑行的距离是24m．
（3）斜坡的高度不应超过25m．
mgsin37°-μmgcos37°=ma
解得：a=gsin37°-μgcos37°=2m/s2．
（2）设人
从斜坡滑道B点的速度为v，由运动学公式得：2as=v2 在水平滑道上做加速运动，加速度：a1=μg=5m/s
设在水平滑道上滑行的距离为S1，由运动学公式得：2a1s1=v2
由以上各式联立解得：S1=24m
（3）设斜坡倾角为θ，斜坡的最大高度为h，滑到底端时的速度为v，则：
v2=2a
| h |
| sinθ |
沿BC前进时的加速度：a′=μg，
沿BC滑行的距离：L=
| v2 |
| 2a′ |
为确保安全要求，则：L+hcotθ≤S．
联立解得：h≤25m．
答：（1）人在斜坡上下滑的加速度大小为2m/s2．
（2）人在水平滑道上滑行的距离是24m．
（3）斜坡的高度不应超过25m．
点评：加速度是联系力学和运动学的桥梁，解决本题的关键进行正确的受力分析，根据牛顿第二定律求出加速度．本题也可以通过动能定理进行求解．
练习册系列答案
相关题目
