题目内容
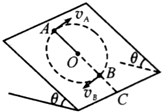 (2011?宜兴市模拟)如图所示,在倾角为θ的光滑斜面上,有一长为l的细线,细线的一端固定在O点,另一端拴一质量为m的小球.已知O点到斜面底边的距离sOC=L.
(2011?宜兴市模拟)如图所示,在倾角为θ的光滑斜面上,有一长为l的细线,细线的一端固定在O点,另一端拴一质量为m的小球.已知O点到斜面底边的距离sOC=L. (1)试证明小球只要能在光滑斜面上做完整的圆周运动,则在最高点A和最低点B时细线上拉力之差为恒量.
(2)若小球恰好能在斜面上做完整的圆周运动,小球运动到A点或B点时细线断裂,若两种情况下小球滑落到斜面底边时到C点的距离相等,则l和L应满足什么关系?
分析:(1)小球从最高点运动到最低点机械能守恒,列出等式表示出小球在A、B两点时的速度分别为vA、vB
的关系.在A、B两点对小球进行受力分析,根据牛顿第二定律求解.
(2)小球恰好能在斜面上做完整的圆周运动,则小球通过A点时细线的拉力为零.根据圆周运动规律和牛顿第二定律求出A点速度.小球从A点运动到B点,根据机械能守恒定律列出等式求出B点速度.小球运动到A点火B点时细线断裂,小球在平行于底边的方向上匀速运动,在垂直于底边的方向上做初速为零的匀加速运动,根据运动规律求解.
的关系.在A、B两点对小球进行受力分析,根据牛顿第二定律求解.
(2)小球恰好能在斜面上做完整的圆周运动,则小球通过A点时细线的拉力为零.根据圆周运动规律和牛顿第二定律求出A点速度.小球从A点运动到B点,根据机械能守恒定律列出等式求出B点速度.小球运动到A点火B点时细线断裂,小球在平行于底边的方向上匀速运动,在垂直于底边的方向上做初速为零的匀加速运动,根据运动规律求解.
解答:解:(1)设小球在A、B两点时的速度分别为vA、vB
则由机械能守恒:
mvB2=
mvA2+mg?2lsinθ
在A点:TA+mgsinθ=m
在B点:TB-mgsinθ=m
则A、B两点拉力之差TB-TA=6mgsinθ 此为一恒量
(2)小球恰好能在斜面上做完整的圆周运动,则小球通过A点时细线的拉力为零.根据圆周运动规律和牛顿第二定律有 mgsinθ=m
,
解得 vA=
.
小球从A点运动到B点,根据机械能守恒定律有
m
+mg?2lsinθ=
m
,
解得 vB=
.
小球运动到A点火B点时细线断裂,小球在平行于底边的方向上匀速运动,在垂直于底边的方向上做初速为零的匀加速运动(类平抛运动).
细线在A点断裂:L+l=
a
,sA=vAtA,
细线在B点断裂:L-l=
a
,sB=vBtB,
又 sA=sB,联立解得 L=
l.
答:(1)证明过程在上面.
(2)l和L应满足关系是L=
l.
则由机械能守恒:
| 1 |
| 2 |
| 1 |
| 2 |
在A点:TA+mgsinθ=m
| vA2 |
| l |
在B点:TB-mgsinθ=m
| vB2 |
| l |
则A、B两点拉力之差TB-TA=6mgsinθ 此为一恒量
(2)小球恰好能在斜面上做完整的圆周运动,则小球通过A点时细线的拉力为零.根据圆周运动规律和牛顿第二定律有 mgsinθ=m
| ||
| l |
解得 vA=
| glsinθ |
小球从A点运动到B点,根据机械能守恒定律有
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
解得 vB=
| 5glsinθ |
小球运动到A点火B点时细线断裂,小球在平行于底边的方向上匀速运动,在垂直于底边的方向上做初速为零的匀加速运动(类平抛运动).
细线在A点断裂:L+l=
| 1 |
| 2 |
| t | 2 A |
细线在B点断裂:L-l=
| 1 |
| 2 |
| t | 2 B |
又 sA=sB,联立解得 L=
| 3 |
| 2 |
答:(1)证明过程在上面.
(2)l和L应满足关系是L=
| 3 |
| 2 |
点评:本题的综合性较强,要了解物体做圆周运动的特点,同时也用到了类平抛的知识和机械能守恒,是一个很好的综合题目,很能考查学生的分析解题能力.

练习册系列答案
相关题目
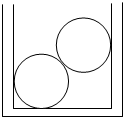 (2011?宜兴市模拟)直径为D的圆柱形桶内放入两个直径为d(2d>D)的光滑圆球,如图所示,其中只与球的重力有关而与桶的直径D无关的力是( )
(2011?宜兴市模拟)直径为D的圆柱形桶内放入两个直径为d(2d>D)的光滑圆球,如图所示,其中只与球的重力有关而与桶的直径D无关的力是( ) (2011?宜兴市模拟)一个机要仓库有一扇很大的电动仓库门,门上装有三把锁,三个机要员各有一把锁的钥匙,只有三人同时转动自己的钥匙(闭合自己的开关),才能通过一个继电器把门打开.图中的S1、S2、S3是三个锁内的开关,J为继电器(图中未画电动机的电路).则方框内符合要求的门电路是( )
(2011?宜兴市模拟)一个机要仓库有一扇很大的电动仓库门,门上装有三把锁,三个机要员各有一把锁的钥匙,只有三人同时转动自己的钥匙(闭合自己的开关),才能通过一个继电器把门打开.图中的S1、S2、S3是三个锁内的开关,J为继电器(图中未画电动机的电路).则方框内符合要求的门电路是( ) (2011?宜兴市模拟)酒精测试仪用于对机动车驾驶人员是否酒后驾车及其他严禁酒后作业人员的现场检测,它利用的是一种二氧化锡半导体型酒精气体传感器.酒精测试仪的工作原理如图所示,其中P是半导体型酒精气体传感器,该传感器电阻r′的倒数与酒精气体的浓度C成正比,R0为定值电阻.以下关于电压表示数的倒数与酒精气体浓度的倒数之间关系的图象,正确的是( )
(2011?宜兴市模拟)酒精测试仪用于对机动车驾驶人员是否酒后驾车及其他严禁酒后作业人员的现场检测,它利用的是一种二氧化锡半导体型酒精气体传感器.酒精测试仪的工作原理如图所示,其中P是半导体型酒精气体传感器,该传感器电阻r′的倒数与酒精气体的浓度C成正比,R0为定值电阻.以下关于电压表示数的倒数与酒精气体浓度的倒数之间关系的图象,正确的是( )