题目内容
已知地球半径为R，地球的同步卫星离地心的距离为r，设第一宇宙速度为V1，地球赤道上的物体随地球自转的向心加速度为a1；同步卫星的线速度为V2，向心加速度为a2，求
和
各为多少？
| V1 |
| V2 |
| a1 |
| a2 |
分析：同步卫星的周期与地球的自转周期相同，根据a=rω2得出同步卫星和随地球自转物体的向心加速度之比，根据万有引力提供向心力得出第一宇宙速度与同步卫星的速度之比．
解答：解：由万有引力等于向心力有：G
=m
从而有 V=
所以
=
因同步卫星与地球自转角速度相同，所以
=
=
答：
为
，
为
．
| Mm |
| r2 |
| V2 |
| r |
从而有 V=
|
所以
| V1 |
| V2 |
|
因同步卫星与地球自转角速度相同，所以
| a1 |
| a2 |
| ωR |
| ωr |
| R |
| r |
答：
| V1 |
| V2 |
|
| a1 |
| a2 |
| R |
| r |
点评：解决本题的关键知道同步卫星和随地球自转的物体角速度相等，同步卫星以及贴近地球表面运行的卫星靠万有引力提供向心力．
练习册系列答案
相关题目
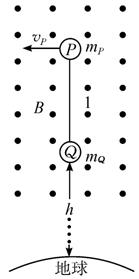
（2005?北京）近期《科学》中文版的文章介绍了一种新技术--航天飞缆，航天飞缆是用柔性缆索将两个物体连接起来在太空飞行的系统．飞缆系统在太空飞行中能为自身提供电能和拖曳力，它还能清理“太空垃圾”等．从1967年至1999年的17次试验中，飞缆系统试验已获得部分成功．该系统的工作原理可用物理学的基本定律来解释．如图为飞缆系统的简化模型示意图，图中两个物体P、Q的质量分别为mP、mQ，柔性金属缆索长为l，外有绝缘层，系统在近地轨道作圆周运动．运动过程中Q距地面高为h．设缆索总保持指向地心，P的速度为vP．已知地球半径为R，地面的重力加速度为g．
