题目内容
有两个相同的总电阻为9 Ω的均匀光滑圆环,固定于一个绝缘的水平台面上,两环分别在两个互相平行的、相距为20 cm的竖直平面内,两环的连心线恰好与环面垂直,两环面间有方向竖直向下的磁感应强度B=0.87 T的匀强磁场,两环的最高点A和C间接有一内阻为0.5 Ω的电源,连接导线的电阻不计.今有一根质量为10 g,电阻为1.5 Ω的棒置于两环内侧且可顺环滑动,而棒恰好静止于图所示的水平位置,它与圆弧的两接触点P、Q和圆弧最低点间所夹的弧所对应的圆心角均为θ=60°,取重力加速度为g=10 m/s2,试求此电源电动势E的大小.
6 V
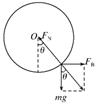
【解析】在图中,从左向右看,棒PQ的受力如图所示,棒所受的重力和安培力FB的合力与环对棒的弹力FN
是一对平衡力,且FB=mgtanθ=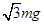
而FB=IBL,所以
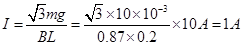
在图所示的电路中两个圆环分别连入电路中的电阻为R,则

由闭合电路欧姆定律得
E=I(r+2R+R棒)=1×(0.5+2×2+1.5)V=6 V.
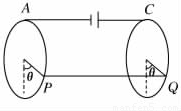
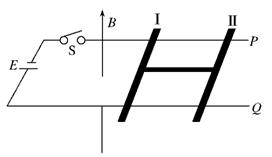
12. 【题文】如图所示,表面光滑的平行金属导轨P、Q水平放置,左端与一电动势为E,内阻为r的电源连接.导轨间距为d,电阻不计.导轨上放有两根质量均为m的细棒,棒Ⅰ电阻为R,棒Ⅱ为绝缘体,两棒之间用一轻杆相连.导轨所在的空间有垂直导轨平面竖直向上的匀强磁场,磁感应强度大小为B.求:
(1)闭合开关S瞬间棒Ⅱ的加速度;
(2)从闭合开关S到两棒速度达到v的过程中,通过棒Ⅰ的电荷量和电源消耗的总能量分别为多少?(导轨足够长)
【答案】(1)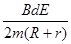 方向水平向右 (2)
方向水平向右 (2)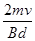
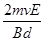
【解析】(1)闭合S的瞬间,电路中的电流为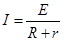
棒Ⅰ受安培力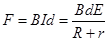
对棒Ⅰ、棒Ⅱ整体,根据牛顿第二定律得
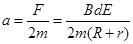 方向水平向右.
方向水平向右.
(2)对棒Ⅰ棒Ⅱ整体,由动量定理
BI′dt=2mv,q=I′·t
∴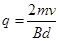
电源消耗的电能为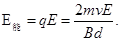

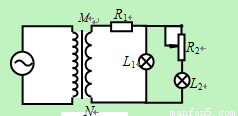
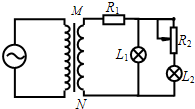 如图所示,理想变压器的输入端接正弦交流电,副线圈上通过输电线接有两个相同的灯泡L1和L2,输电线的等效电阻为R1.当滑动变阻器R2的滑片P向下滑动时,以下说法中正确的是( )
如图所示,理想变压器的输入端接正弦交流电,副线圈上通过输电线接有两个相同的灯泡L1和L2,输电线的等效电阻为R1.当滑动变阻器R2的滑片P向下滑动时,以下说法中正确的是( )