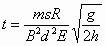题目内容
两块厚度不同的木板并在一起,直立固定在地面上。一颗子弹水平射向木板,恰好把这两块木板射穿。已知它通过这两块木板所用时间之比为1:2,并且子弹通过这两块木板时受到的阻力大小相等,求这两块木板的厚度之比。
5:4
设子弹初速度为v0, 子弹刚射穿第一块木板时速度为v1, 则
I1:I2=Δp1:Δp2=m(v0-v1):m(v1-0)=1:2,
可解出 v1=2 v0/3。
因为 s=Δv/2a, 因此
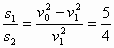 。
。本题也可以运用初速为零的匀变速直线运动的规律求解:倒过来看,它的运动就是初速为零的匀变速直线运动,相邻相等时间间隔内的位移之比为1:3:5:………现在后一块木板占两份时间,第一块木板占一份时间,因此两块木板的厚度之比为5:(3+1)=5:4。

练习册系列答案
相关题目
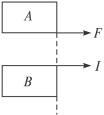
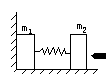
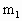 =0.5kg,
=0.5kg,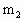 =1.49kg的两个物体,置于光滑水平面上,
=1.49kg的两个物体,置于光滑水平面上,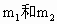 都将向右运动,试求:
都将向右运动,试求: