Ő‚ńŅńŕ»›
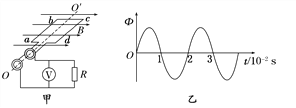
°ĺŐ‚ńŅ°Ņ“ĽĺÝ‘Ķ–®–őőÔŐŚĻŐ∂®‘ŕňģ∆Ĺ√ś…Ō£¨◊ů”“ŃĹ–Ī√ś”Žňģ∆Ĺ√śĶńľ–Ĺ«∑÷Īūő™¶ŃļÕ¶¬£¨¶Ń£Ĺ37°„°Ę¶¬£Ĺ53°„.»ÁÕľňý ĺ£¨Ō÷į—ŃĹłý÷ ŃŅĺýő™m°ĘĶÁ◊Ťő™ĺýR°Ę≥§∂»ĺýő™LĶńĹū ŰįŰĶńŃĹ∂ň”√Ķ»≥§ĶńĶÁ◊Ť≤Ľľ∆ĶńŌł»ŪĶľŌŖѨŔ∆ūņī£¨≤Ęį—ŃĹįŰ∑÷Īū∑Ň‘ŕ–®–őŐŚĶńŃĹłŲĻ‚Ľ¨Ķń–Ī√ś…Ō£¨‘ŕ’ŻłŲ–®–őŐŚĶń«Ý”Úńŕīś‘ŕ∑ĹŌÚ ķ÷ĪŌÚ…Ō°ĘīŇł–”¶«Ņ∂»ő™BĶń‘»«ŅīŇ≥°£¨‘ŕŌł»ŪĶľŌŖł’ļ√ņ≠÷Īļů”…ĺ≤÷Ļ Õ∑ŇŃĹĹū ŰįŰ£¨≤Ľľ∆“Ľ«–ń¶≤Ń◊ŤŃ¶£¨Ōł»ŪĶľŌŖ◊„ĻĽ≥§£¨ŃĹĶľŌŖ“Ľ÷Ī‘ŕ–Ī√ś…Ō£¨sin 37°„£Ĺ0.6£¨cos 37°„£Ĺ0.8£¨÷ōѶľ”ňŔ∂»ő™g.

(1)«ůĹū ŰįŰĶń◊Óīůľ”ňŔ∂»£Ľ
(2)«ůĹū ŰįŰĶń◊ÓīůňŔ∂»£ģ
°ĺīūįł°Ņ(1) 0.2g (2) ![]()
°ĺĹ‚őŲ°Ņ
‘Ő‚ĶĪĹū ŰįŰł’ Õ∑Ň Ī£¨į≤ŇŗѶő™Ń„£¨īň Īľ”ňŔ∂»◊Óīů£ģŃĹįŰŌ¬Ľ¨Ļż≥Ő£¨Ō»◊Ųľ”ňŔ∂»ľű–°ĶńĪšľ”ňŔ‘ň∂Į£¨◊Óļů◊Ų‘»ňŔ‘ň∂Į£ģ‘»ňŔ‘ň∂Į Ī£¨ňŔ∂»◊Óīů£ģ”…∆Ĺļ‚ŐűľĢļÕĶÁīŇł–”¶÷™ ∂Ņ…«ů≥Ų◊ÓīůňŔ∂»°£
(1)łýĺ›Ň£∂ŔĶŕ∂Ģ∂®¬…£ļmg(sin¶¬£≠sin¶Ń)£Ĺma
ĽĮľÚ‘Ú£ļa£Ĺ0.2g
(2)įŰ ‹Ń¶∆Ĺļ‚ Ī£¨ŃĹįŰňŔ∂»v◊Óīů£ģ“ÚŃĹįŰňŔ∂»īů–°ŌŗĶ»£¨Ķę«–łÓBĶń”––ßňŔ∂»≤ĽÕ¨£¨ł–”¶ĶÁŃųĶń∑ĹŌÚő™ńś Ī’Ž
‘Ú‘ŕt Īľšńŕł–”¶ĶÁ∂Į ∆E£Ĺ![]() £ĹBLv(cos¶Ń£≠cos¶¬)
£ĹBLv(cos¶Ń£≠cos¶¬)
∆šł–”¶ĶÁŃų£ļI=![]()
į≤ŇŗѶ£ļFb=IBL
…ŤŌłŌŖ∂‘įŰĶńѶő™F£¨∂‘”“įŰ£ļmgsin¶¬£ęFbcos¶¬£≠F=0
∂‘◊ůįŰ£ļF£≠Fbcos¶Ń£≠mgsin¶Ń=0
Ń™ŃĘĹ‚£ļv=![]()

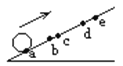
°ĺŐ‚ńŅ°Ņ‘ŕ—–ĺŅ∆ĹŇ◊‘ň∂ĮĶń Ķ—ť÷–£¨ń≥Õ¨—ßľ«¬ľŃň–°«Ú‘ň∂ĮÕĺ÷–ĺ≠ĻżĶńA°ĘB°ĘC°ĘD°ĘE°ĘF°ĘGĶ„ĶńőĽ÷√£¨ŌŗŃŕŃĹĶ„Ķń ĪľšľšłŰĺýő™![]() =0.05s°£»°AĶ„ő™◊ÝĪÍ‘≠Ķ„£¨“‘+x∑ĹŌÚĪŪ ĺňģ∆Ĺ≥űňŔ∂»∑ĹŌÚ°Ę+y∑ĹŌÚĪŪ ĺ ķ÷ĪŌÚŌ¬∑ĹŌÚ£¨ Ķ—ťľ«¬ľ»ÁŌ¬£ļ£®ĹŠĻŻĪ£ŃŰŃĹőĽ–° ż£©
=0.05s°£»°AĶ„ő™◊ÝĪÍ‘≠Ķ„£¨“‘+x∑ĹŌÚĪŪ ĺňģ∆Ĺ≥űňŔ∂»∑ĹŌÚ°Ę+y∑ĹŌÚĪŪ ĺ ķ÷ĪŌÚŌ¬∑ĹŌÚ£¨ Ķ—ťľ«¬ľ»ÁŌ¬£ļ£®ĹŠĻŻĪ£ŃŰŃĹőĽ–° ż£©
ĪÍļŇn | A | B | C | D | E | F | G |
t£®s£© | 0 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 |
x£®m£© | 0 | 0.024 | 0.051 | 0.073 | 0.098 | 0.126 | 0.150 |
y£®m£© | 0 | 0.042 | 0.108 | 0.198 | 0.314 | 0.454 | 0.617 |

£®1£©◊ų≥Ųx°™tÕľŌů»ÁÕľ1ňý ĺ£¨–°«Ú∆ĹŇ◊‘ň∂ĮĶńňģ∆Ĺ≥űňŔ∂»īů–° «______m/s£Ľ
£®2£©“‘tő™ļŠ◊ÝĪÍ£¨![]() ő™◊›◊ÝĪÍ£¨◊ų≥Ų
ő™◊›◊ÝĪÍ£¨◊ų≥Ų![]() °™tÕľŌů»ÁÕľ2ňý ĺ£¨∆šļĮ żĹ‚őŲ Ĺő™
°™tÕľŌů»ÁÕľ2ňý ĺ£¨∆šļĮ żĹ‚őŲ Ĺő™![]() = 4.88t + 0.59£ļ
= 4.88t + 0.59£ļ
ĘŔ÷ōѶľ”ňŔ∂»Ķń≤‚ŃŅ÷Ķ «________m/s£Ľ
Ęŕt=0.10s Ī£¨–°«ÚĶń ķ÷Ī∑÷ňŔ∂»īů–° «_________m/s£Ľ