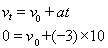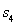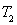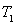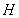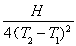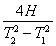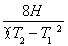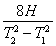题目内容
运动场上4×800m接力赛已进入了白热化阶段,甲、乙两队都已经是最后一棒。甲队员健步如飞,最大速度达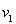 =12m/s,乙队员也不甘落后奋力直追,可能是由于紧张,甲队员不小心将接力棒失落,回头拾起棒后,甲加速直追反超乙。现将甲的加速和减速过程都视为匀变速运动,且加速时的加速度大小
=12m/s,乙队员也不甘落后奋力直追,可能是由于紧张,甲队员不小心将接力棒失落,回头拾起棒后,甲加速直追反超乙。现将甲的加速和减速过程都视为匀变速运动,且加速时的加速度大小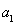 =2m/s2,减速时的加速度大小
=2m/s2,减速时的加速度大小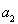 =6m/s2,拾棒时的速度为零,不计棒脱手后的位移和拾棒动作所花的时间,问:(1)甲在返回拾棒过程中的最大速率为多少?
=6m/s2,拾棒时的速度为零,不计棒脱手后的位移和拾棒动作所花的时间,问:(1)甲在返回拾棒过程中的最大速率为多少?
(2)甲因为拾棒而耽误了多少时间?
(3)若丢棒时甲领先乙△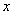 =8m,而距离终点
=8m,而距离终点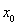 =240m,乙的速度保持
=240m,乙的速度保持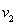 =10m/s,通过计算分析甲能否赢得比赛?
=10m/s,通过计算分析甲能否赢得比赛?
(1)6m/s(2)9s(3)甲能赢得比赛
【解析】
试题分析:(1)丢棒后,甲先减速至零,其时间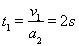 ,
,
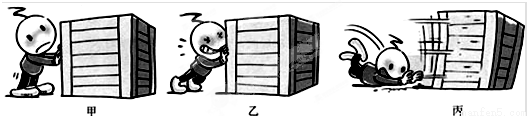
位移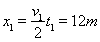
之后反向加速,再减速至零,设最大速度为vm,则有: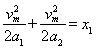 ,解得:vm=6m/s
,解得:vm=6m/s
(2)返回拾棒过程的时间为 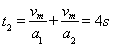
再继续加速前进到达最大速度的过程中,其时间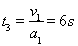
位移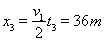
若是没丢棒,跑这段位移的时间 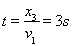
故耽误的时间为 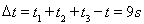
(3) 从掉棒开始计时,甲到终点需要的时间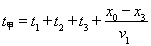 = 29s
= 29s
乙到终点需要的时间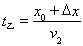 =32s
=32s
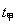 <
<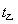 ,说明最终甲能赢得比赛。
,说明最终甲能赢得比赛。
考点:匀变速运动的规律。

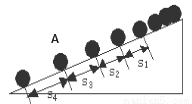
(4分)一个小球沿斜面向下运动,现在用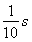 的闪频相机拍摄下的不同时刻的小球所处的位置照片如图所示,测得小球的在连续相等的时间内的位移如下表,则:
的闪频相机拍摄下的不同时刻的小球所处的位置照片如图所示,测得小球的在连续相等的时间内的位移如下表,则:
|
|
|
|
8.20cm | 9.30cm | 10.40cm | 11.50cm |
(1)小球在相邻的相等时间内的位移差 (填写“相等”或“不相等”),小球的运动性质属于 直线运动.
(2)有甲、乙两个同学计算小球的加速度的方法如下:
甲: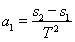 ,
,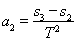 ,
,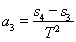 ,
,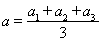 ;
;
乙: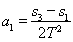 ,
,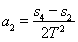 ,
,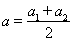 ;
;
撇开本题所给的数据从理论上讲,甲、乙两位同学的计算方法中 (填写“甲、乙”)方法更好.