题目内容
16.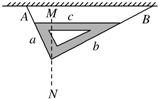 如图所示,一个教学用的直角三角板的边长分别为a、b、c,被沿两直角边的细绳A、B悬吊在天花板上,且斜边c恰好平行天花板,过直角的竖直线为MN.设A、B两绳对三角形薄板的拉力分别为Fa和Fb,已知Fa和Fb及薄板的重力为在同一平面的共点力,则下列判断正确的是( )
如图所示,一个教学用的直角三角板的边长分别为a、b、c,被沿两直角边的细绳A、B悬吊在天花板上,且斜边c恰好平行天花板,过直角的竖直线为MN.设A、B两绳对三角形薄板的拉力分别为Fa和Fb,已知Fa和Fb及薄板的重力为在同一平面的共点力,则下列判断正确的是( )| A. | 薄板的重心不在MN线上 | B. | $\frac{Fa}{Fb}$=$\frac{a}{b}$ | ||
| C. | $\frac{Fa}{Fb}$=$\frac{b}{a}$ | D. | $\frac{Fa}{Fb}$=$\frac{b}{c}$ |
分析 根据三力汇交原理确定重心的位置,根据合力为零,运用合成法求出Fa和Fb的比值.
解答 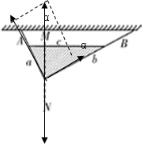 解:A、B、三角形薄板受重力、两个拉力处于平衡,三个力虽然不是作用在同一点,根据三力汇交原理,三个力的延长线必然交于一点,由几何关系,三个力一定交于三角形下面的顶点,所以重心一定在MN线上.故A错误.
解:A、B、三角形薄板受重力、两个拉力处于平衡,三个力虽然不是作用在同一点,根据三力汇交原理,三个力的延长线必然交于一点,由几何关系,三个力一定交于三角形下面的顶点,所以重心一定在MN线上.故A错误.
A、C、三角形薄板受力分析如图,根据合力等于0,则Fa=mgcosα,Fb=mgsinα,则$\frac{{F}_{a}}{{F}_{b}}$=cotα=$\frac{b}{a}$.故C正确,BD错误.
故选:C.
点评 解决本题的关键理解共点力,能够正确地进行受力分析,运用共点力平衡进行求解.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
4.光滑水平地面上叠放两物块a,b,ma=4kg,mb=16kg,弹簧右端固定在b上,左端拉住a,a、b均处于静止状态,此时弹簧的拉力为3N.现对b施加水平向右的拉力F,F随时间t变化的图象如图所示,则( )
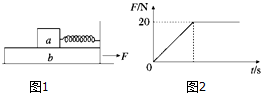

| A. | a与b始终保持相对静止 | |
| B. | a受到的摩擦力先减小、后增大再不变 | |
| C. | a受到的摩擦力先向左、后向右 | |
| D. | 当F=20N时,a受到的摩擦力为4N |
4.已知船速V船大于水速V水,欲横渡宽为L河:以下说法正确的是( )
①船头垂直河岸正对彼岸航行时,横渡时间最短;
②船头垂直河岸正对彼岸航行时,实际航程最短;
③船头朝上游转过一定角度,使实际航线垂直河岸,此时航程最短;
④船头朝下游转过一定角度,使实际航程增大,此时渡河时间最短.
①船头垂直河岸正对彼岸航行时,横渡时间最短;
②船头垂直河岸正对彼岸航行时,实际航程最短;
③船头朝上游转过一定角度,使实际航线垂直河岸,此时航程最短;
④船头朝下游转过一定角度,使实际航程增大,此时渡河时间最短.
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
11.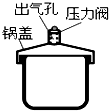 如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )
如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )
 如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )
如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )| A. | 压强增大 | B. | 内能不变 | ||
| C. | 对外界做正功 | D. | 分子平均动能增大 | ||
| E. | 对外没有做功 |
1. 运动员手持网球拍托球沿水平面匀加速跑,设球拍和球质量分别为M、m球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
运动员手持网球拍托球沿水平面匀加速跑,设球拍和球质量分别为M、m球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
 运动员手持网球拍托球沿水平面匀加速跑,设球拍和球质量分别为M、m球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
运动员手持网球拍托球沿水平面匀加速跑,设球拍和球质量分别为M、m球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )| A. | 运动员的加速度为gcotθ | |
| B. | 球拍对球的作用力$\frac{mg}{cosθ}$ | |
| C. | 运动员对球拍的作用力为Mgcosθ | |
| D. | 若加速度大于gsinθ,球一定沿球拍向上运动 |
5.在离地面80m处无初速释放一小球,小球质量为m=200g,不计空气阻力,g取10m/s2,取最高点所在水平面为参考平面,则第2s末小球的重力势能为( )
| A. | 40J | B. | -40J | C. | 120J | D. | -120J |