��Ŀ����
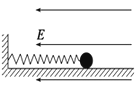
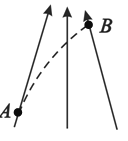
����Ŀ����ͼ��ʾ��������ȫ��ͬ��С���飨����Ϊ�ʵ㣩ͨ�������쳤��ϸ������ˮƽƽ̨�ϵ�С��O���ӣ���һ����B������ƽ̨����Aһ���ٶȣ�ʹ������O��������Բ���˶���B�պÿ��Ա��־�ֹ����ƽ̨֮����ѹ���ڶ��ν�B��λ������������ƽ̨�߶�Ϊ����������֮һ�����ٴ���A����O��������Բ���˶���B��Ȼ���Ա��־�ֹ������һ��Ħ����ƽ̨��ȿ��Ժ��ԣ���������A������Բ���˶������ٶȺ�����֮�ȣ�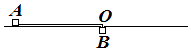
���𰸡��⣺�����ӵ�������СΪF��ϸ���ij���Ϊl������B�����־�ֹ�������У�F��mg=0
��һ�Σ���A�����ٶ�Ϊv1������ΪT1����ʱ�뾶Ϊl�����Ӷ�A�������ṩ���������У�
F= ![]()
T1= ![]()
�ڶ��Σ���A�����ٶ�Ϊv2������ΪT2����ʱ�뾶Ϊ ![]() l�����Ӷ�A�������ṩ���������У�
l�����Ӷ�A�������ṩ���������У�
F= ![]()
T2= ![]()
�������ϸ�ʽ����ã�
![]()
![]()
��������A������Բ���˶������ٶ���֮��Ϊ ![]() ������֮��Ϊ
������֮��Ϊ ![]()
����������������ת����������ٶ���ͬ������������������������Դ���������������ٶȹ�ϵ��ʽ��⡣
�����㾫������������Բ���˶����������ǽ����ĸ�������Ҫ֪������Բ���˶����ٶȵĴ�С�㶨�����ٶȡ����ں�Ƶ�ʶ��Ǻ㶨����ģ����ļ��ٶȺ��������Ĵ�СҲ���Ǻ㶨����ģ����ٶȴ�С������ٶȷ���ʱ���ڱ�ı��������˶�������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�