题目内容
18. 如图所示有一块长为1m的薄木板静止水平地面上,薄木板质量为4㎏,其与地面间的动摩擦因数μ0为0.5,薄木板右端放一质量1kg为小滑块,大小可忽略不计,小滑块与薄木板之间的动摩擦因数为μ1为0.4,小滑块与地面之间的动摩擦因数为μ2为0.2.
如图所示有一块长为1m的薄木板静止水平地面上,薄木板质量为4㎏,其与地面间的动摩擦因数μ0为0.5,薄木板右端放一质量1kg为小滑块,大小可忽略不计,小滑块与薄木板之间的动摩擦因数为μ1为0.4,小滑块与地面之间的动摩擦因数为μ2为0.2.(1)现用水平方向的恒力F拉木板M,为使m能从M上滑落,F需满足的条件;
(2)在其它条件不变,若恒力F=53N,且始终作用在M上,小滑块运动的时间多长;(忽略不计小滑块从薄木板上滑落的时间及速度变化)
(3)在满足(2)的条件中,小滑块静止时距薄木板的左侧距离多大.
分析 (1)小滑块在木板上滑动时,根据牛顿第二定律,求出滑块和木板的加速度,当木板的加速度大于滑块的加速度时,m就会从M上滑落下来.
(2)恒力F=53N,m在M上发生相对滑动,设m在M上面滑动的时间为t,求出木块在t内的位移,两者位移之差等于木板的长度L;
(3)小滑块滑落后,由牛顿第二定律结合受力分析求出二者的加速度,然后求出滑块停止运动的时间,最后由位移公式即可求出.
解答 解:(1)以M、m组成的系统为研究对象.当二者能一起加速运动时满足:F-μ0(M+m)g=(M+m)a
以m为研究对象,其加速度达到最大值时满足:μ1mg=ma1
当a>a1时,M、m可以发生相对运动,即:F>(μ0+μ1)(M+m)g
代入数据得:F>45N
(2)以m在M上发生相对运动为研究过程,根据牛顿第二定律
对m有:μ1mg=ma1
可得:${a_1}={μ_1}g=4m/{s^2}$
对M有:F-μ0(M+m)g-μ1mg=Ma2
可得${a_2}=\frac{{F-{μ_0}(M+m)g-{μ_1}mg}}{M}=6m/{s^2}$
由题意可得M、m的运动关系满足:L=x2-x1
根据${x_1}=\frac{1}{2}{a_1}{t^2}$,可得m对地位移;${x_2}=\frac{1}{2}{a_2}{t^2}$可得M对地位移
所以$t=\sqrt{\frac{2L}{{a}_{2}-{a}_{1}}}$
代入数据得:t=1s
此时,m落地时的速度为v1满足:v1=a1t=4×1=4m/s
M此时的速度v2满足:v2=a2t=6×1=6m/s
以m在地面上滑行为研究过程,由牛顿第二定律μ2mg=ma'1
可得:a'1=μ2g=0.2×10=2m/s2
由v1=a'1t'
可得,m的滑行时间t'=2s
所以小滑块运动的时间t总=t+t'=1+2=3s
(3)以M、m分别在地面上运动为研究过程,
根据$2{a'_1}{x'_1}=v_1^2$
可得在地面上滑行距离$x{′}_{1}=\frac{{v}_{1}^{2}}{2{a′}_{1}}=\frac{{4}^{2}}{2×2}=4m$
对M根据牛顿第二定律:F-μ0Mg=Ma'2可得:$a{′}_{2}=\frac{F-{μ}_{0}Mg}{M}$
根据${x'_2}={v_2}t'+\frac{1}{2}{a'_2}{t'^2}$
代入数据可得:x'2=28.5m
由题意可知,所求间距△x满足:△x=x'2-x'1=18.5-4=24.5m
答:(1)现用水平方向的恒力F拉木板M,为使m能从M上滑落,F需满足的条件是F>45N;
(2)在其它条件不变,若恒力F=53N,且始终作用在M上,小滑块运动的时间长3s;
(3)在满足(2)的条件中,小滑块静止时距薄木板的左侧距离多大.
点评 解决本题的关键知道滑块在薄木板上发生相对滑动时,薄木板的加速度大于滑块的加速度.以及知道滑块在薄木板上滑下时,两者的位移之差等于滑板的长度.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案 如图所示,A、B为相同的两个木块,叠放在水平地面C上.A、B用水平绳通过一个滑轮连接在一起.在滑轮上用一个水平力F,恰好使A、B两个木块一起沿水平地面向右匀速运动,不计轻绳和滑轮的质量以及滑轮轴的摩擦,关于A、B间的摩擦力f1和B、C间的摩擦力f2的大小.下列判断正确( )
如图所示,A、B为相同的两个木块,叠放在水平地面C上.A、B用水平绳通过一个滑轮连接在一起.在滑轮上用一个水平力F,恰好使A、B两个木块一起沿水平地面向右匀速运动,不计轻绳和滑轮的质量以及滑轮轴的摩擦,关于A、B间的摩擦力f1和B、C间的摩擦力f2的大小.下列判断正确( )| A. | f1=$\frac{F}{2}$,f2=$\frac{F}{2}$ | B. | f1=$\frac{F}{2}$,f2=F | ||
| C. | f1=0,f2=F | D. | 条件不足,无法判断 |
| A. | 由E=$\frac{F}{q}$可知,电场强度E跟放入的电荷q所受的电场力成正比 | |
| B. | 在以点电荷为圆心,r为半径的球面上,各点的场强都相同 | |
| C. | 电场线是客观存在的 | |
| D. | 电场线上某点的切线方向与电荷在该点受力方向可以不同 |

(1)往砝码盘中加入一小砝码,在释放小车前(选填“前”或“后”)接通打点计时器的电,在纸带上打出一系列的点.
(2)从纸带上选取若干计数点进行测量,得出各计数点的时间t与速度v的数据如上表:
请根据实验数据作出小车的v-t图象乙.
| 时间t/s | 0 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| 速度v(m/s) | 0.12 | 0.19 | 0.23 | 0.26 | 0.28 | 0.29 |

①在本次实验中,实验小组通过改变滑块质量总共做了6组实验,得到如表所示的实验数据.通过分析表中数据后,你得出的结论是在合外力不变的情况下,物体运动的加速度跟物体的质量成反比.
| m(g) | a(m/s2) | ma |
| 250 | 2.02 | |
| 300 | 1.65 | |
| 350 | 1.33 | |
| 400 | 1.25 | |
| 500 | 1.00 | |
| 800 | 0.63 |
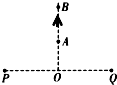 如图所示,在真空中有两个正点电荷,电量相等,分别置于P、Q两点,A、B为P、Q连线的中垂线上的两点,现将一负电荷q由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )
如图所示,在真空中有两个正点电荷,电量相等,分别置于P、Q两点,A、B为P、Q连线的中垂线上的两点,现将一负电荷q由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )| A. | q的电势能逐渐减小 | B. | q的电势能逐渐增大 | ||
| C. | q受到的电场力一定先减小后增大 | D. | q受到的电场力一直做正功 |
| A. |  日全食现象 | B. |  人照镜子 | C. |  树在水中的倒影 | D. |  用放大镜看书 |
 利用如图所示的装置验证机械能守恒定律.图中AB是固定的光滑斜面,斜面的倾角为a,1和2是固定在斜面上适当位置的两个光电门,与它们连接的光电计时器(没有画出)能够显示挡光时间.让滑块从斜面的顶端滑下,光电门1、2各自连接的光电计时器显示的挡光时间分别为t1、t2,已知滑块质量为m,滑块沿斜面方向的长度为L,光电门1和2之间的距离为s,重力加速度为g,取滑块经过光电门时的速度为其平均速度.则:
利用如图所示的装置验证机械能守恒定律.图中AB是固定的光滑斜面,斜面的倾角为a,1和2是固定在斜面上适当位置的两个光电门,与它们连接的光电计时器(没有画出)能够显示挡光时间.让滑块从斜面的顶端滑下,光电门1、2各自连接的光电计时器显示的挡光时间分别为t1、t2,已知滑块质量为m,滑块沿斜面方向的长度为L,光电门1和2之间的距离为s,重力加速度为g,取滑块经过光电门时的速度为其平均速度.则: