题目内容
4.一质点在x轴上运动,在t0=0时质点处于位置x0=0m,然后质点沿x轴正方向运动,在t1=2s时质点处于位置x1=10m,此后质点沿x轴负方向运动,在t2=4s时质点处于位置x2=-10m,求:(1)质点在这4s内的平均速率;
(2)后2s内质点的平均速度;
(3)这4s内的平均速度.
分析 路程表示运动轨迹的长度,位移是矢量,有大小,有方向,可以用由初始位置指向末位置的有向线段表示;平均速率等于路程与时间的比值;而平均速度是一段过程中位移与所用的时间的比值.
解答  解:(1)建立一维坐标系,标出x0、x1、x2的位置如图所示.
解:(1)建立一维坐标系,标出x0、x1、x2的位置如图所示.
质点在这4s内通过的路程 s=x1-x0+|x2-x1|=10m-0+|-10-10|m=30m
则平均速率v=$\frac{s}{t}$=$\frac{30}{4}$=7.5m/s
(2)后2s内质点的位移△x′=x2-x1=-20m
平均速度 $\overline{{v}_{2}}$=$\frac{△x′}{△t′}$=$\frac{-20}{2}$m/s=-10m/s
(3)质点在这4s内通过的位移是△x=x2-x0=-10m
所以质点在这4s内的平均速度 $\overline{{v}_{4}}$=$\frac{△x}{△t}$=$\frac{-10}{4}$m/s=-2.5m/s
答:(1)平均速率为7.5m/s(2)后2s内质点的平均速度为-10m/s;
(3)这4s内的平均速度为-2.5m/s.
点评 解决本题要掌握位移△x=x2-x1,平均速度公式$\overline{v}$=$\frac{△x}{△t}$,并要知道路程与位移的关系.同时明确平均速率与平均速度之间的区别.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
14.关于伽利略对自由落体运动的研究,下列说法错误的是( )
| A. | 伽利略运用逻辑推理的方法否定了“重物比轻物落得快”的结论 | |
| B. | 伽利略创造了实验与逻辑推理相结合的科学研究方法 | |
| C. | 伽利略通过测量自由落体运动的速度和时间得出速度随时间均匀变化 | |
| D. | 伽利略通过研究小球沿斜面向下的运动并进行合理外推,得出自由落体运动规律 |
12.关于惯性在实际中的应用,下列说法中错误的是( )
| A. | 运动员在掷标枪时的助跑是为了利用惯性 | |
| B. | 运动员在跳远时的助跑是为了增大起跳时的惯性 | |
| C. | 手扶拖拉机的飞轮做得很重,是为了增大它转动的惯性 | |
| D. | 战斗机在空战时,甩掉副油箱是为了减小惯性,提高飞行的灵活性 |
9.关于对自由落体运动的认识,下列说法正确的是( )
| A. | 自由落体运动是沿竖直方向的匀加速直线运动 | |
| B. | 亚里士多德认为“重物”和“轻物”下落的同样快 | |
| C. | 自由落体运动在开始连续的三个1s末的速度之比为1:3:5 | |
| D. | 自由落体运动在开始连续的三个2s内的位移之比为1:3:5 |
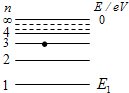 如图所示,有一群氢原子处于量子数n=3的激发态.跃迁过程最多能发出3条光谱线.设基态能量为-E1,普朗克常量为h.这几条谱线中最大频率为$\frac{8{E}_{1}}{9h}$.
如图所示,有一群氢原子处于量子数n=3的激发态.跃迁过程最多能发出3条光谱线.设基态能量为-E1,普朗克常量为h.这几条谱线中最大频率为$\frac{8{E}_{1}}{9h}$.
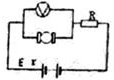 如图所示电路,电动机的线圈电阻是1Ω,电动机工作时电压表的示数是12V,电池组的电动势是22V,内电阻是1Ω,电阻R的阻值为4Ω.不考虑电压表对电路的影响.求:
如图所示电路,电动机的线圈电阻是1Ω,电动机工作时电压表的示数是12V,电池组的电动势是22V,内电阻是1Ω,电阻R的阻值为4Ω.不考虑电压表对电路的影响.求:
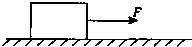 如图所示,用F=2.0N的水平拉力,使质量m=2.0kg的物体由静止开始沿光滑水平面做匀加速直线运动.求:
如图所示,用F=2.0N的水平拉力,使质量m=2.0kg的物体由静止开始沿光滑水平面做匀加速直线运动.求: