题目内容
6.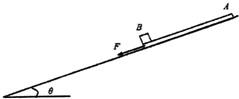 如图所示,倾角为θ=37°的足够长的斜面上放置有一长度为l=2.5m、质量为m1=1kg的木板A,木板A的上表面放有一质量为m2=2kg物块B.木板A与斜面间的动摩擦因数μ1=0.8,物块B与木板A间的动摩擦因数μ2=0.5.开始时物块B刚好在木板A的下端,在木板上施加沿斜面向下、大小为35.2N的恒力F,两者由静止开始运动起来.重力加速度取g=10m/s2,sin37°=0.6,则:
如图所示,倾角为θ=37°的足够长的斜面上放置有一长度为l=2.5m、质量为m1=1kg的木板A,木板A的上表面放有一质量为m2=2kg物块B.木板A与斜面间的动摩擦因数μ1=0.8,物块B与木板A间的动摩擦因数μ2=0.5.开始时物块B刚好在木板A的下端,在木板上施加沿斜面向下、大小为35.2N的恒力F,两者由静止开始运动起来.重力加速度取g=10m/s2,sin37°=0.6,则:(1)由静止开始运动1s时.求A、B的相对位移
(2)为了不让物块B从木板A上滑出,可以在1s后使F的大小改变为另一定值F′(方向不变),则F′需满足什么条件?
分析 (1)分别对AB进行分析,根据牛顿第二定律及运动学公式可求各自的位移,则可求得相对位移;
(2)根据题意明确明确两物体的运动状态的改变;利用牛顿第二定律确定各自的加速度,利用相对位移关系确定如何才能不滑出;从而确定力的大小范围.
解答 解:(1)设A的加速度为a1,对A分析有:
F+m1gsinθ-f-f斜=m1a1;
代入数据解得:a1=14m/s2;
设B的加速度为a2,对B分析可知:
f+m2gsinθ;
代入据解得:a2=10m/s2;
其中f=μ2m2gcosθ;
f斜=μ1(m1+m2)gcosθ;由静止开始运动1s时,A的位移为:xA=$\frac{1}{2}{a}_{1}{t}^{2}$=$\frac{1}{2}×14×1$=7m;
B的位移为:xB=$\frac{1}{2}{a}_{2}{t}^{2}$=$\frac{1}{2}×10×1$=5m;
故AB相对位移为2m;
此时A的速度为14m/s;B的速度为10m/s.
(2)在1s后F的大小变为F′,分析知,B仍然做加速度a2=10m/s2的匀加速运动,要满足B不从A上滑出,则A一定要减速,设其加速度大小为a3,设经过t′时间后AB共速为VB,对A有:v共=vA-a3t′;
对B有:v共=vB+a2t′
该段时间内的位移,sA=vAt′-$\frac{1}{2}$a3t′2
B的位移sB=vBt′+$\frac{1}{2}{a}_{2}t{′}^{2}$
且有:sA-sB≤0.5
联立上式可得:v共=11.5m/s;
t′≤0.25s
a3≥6m/s2;
对A受力分析有:
f+f斜-(F′+m1gsinθ)=m1a3
解得:F′≤15.2N;
当AB共速后又要保证不再发生相对滑动,设AB整体加速度为a′,则对AB整体有:
F′+(m1+m2)gsinθ-f斜=(m1+m2)a′
对A有m2gsinθ-f斜=m2a′
且f静≤f
联立上式解得:F′≥7.2N;
则有:
7.2N≤F′≤15.2N;
答:(1)由静止开始运动1s时.A、B的相对位移为2m;
(2)为了不让物块B从木板A上滑出,可以在1s后使F的大小改变为另一定值F′(方向不变),则F′需满足7.2N≤F′≤15.2N;
点评 本题考查牛顿第二定律的综合应用,涉及两个物体的多个过程,难度较大;要求能正确做好受力分析和过程分析,明确各过程中牛顿第二定律及运动学公式的应用;注意掌握加速度这一桥梁作用.

 如图所示,水平放置的传送带足够长,它以恒定速率v逆时针运行,一小物体以水平向右的初速度v0滑上A端,物体与传送带间的动摩擦因数为μ.物体离开传送带前,以下说法正确的是( )
如图所示,水平放置的传送带足够长,它以恒定速率v逆时针运行,一小物体以水平向右的初速度v0滑上A端,物体与传送带间的动摩擦因数为μ.物体离开传送带前,以下说法正确的是( )| A. | 如果v0=v,物体一定受到摩擦力的作用 | |
| B. | 如果v0>v,物体将先减速运动再匀速运动 | |
| C. | 如果v0<v,物体将先向右做减速运动再向左做加速运动 | |
| D. | 如果v0<v,物体将先加速运动再匀速运动 |
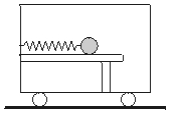 沿平直轨道运动的火车车厢中的光滑水平桌面上用弹簧拴着一个小球,弹簧处于自然长度,如图所示,当旅客看到弹簧的长度变长时,对火车运动状态的判断可能正确的是( )
沿平直轨道运动的火车车厢中的光滑水平桌面上用弹簧拴着一个小球,弹簧处于自然长度,如图所示,当旅客看到弹簧的长度变长时,对火车运动状态的判断可能正确的是( )| A. | 向右运动,速度在增大 | B. | 向右运动,速度在减小 | ||
| C. | 向左运动,速度在增大 | D. | 向左运动,速度在减小 |
 如图所示,表示一个电场中 a、b、c、d 四点分别引入检验电荷时,测得它所受的电场力跟检验电荷的电量的函数关系图象,那么下列说法中正确的是( )
如图所示,表示一个电场中 a、b、c、d 四点分别引入检验电荷时,测得它所受的电场力跟检验电荷的电量的函数关系图象,那么下列说法中正确的是( )| A. | 这个电场是非匀强电场 | |
| B. | a、b、c、d四点的场强大小关系是 E d>E a>E b>E c | |
| C. | a、b、c、d四点的场强大小关系是E a>E b>E c>E d | |
| D. | 无法确定这四个点的场强大小关系 |
| A. | 3r | B. | $\frac{1}{3}$r | C. | $\sqrt{3}$r | D. | $\frac{\sqrt{3}}{3}$r |
 如图所示,固定在竖直平面内的光滑细杆MN,是按照以初速度v0平抛的运动轨迹制成,M端为抛出点,MN间竖直方向高度差为h.现将一小球套于其上,由静止开始从M端沿杆滑下,已知重力加速度为g,则有( )
如图所示,固定在竖直平面内的光滑细杆MN,是按照以初速度v0平抛的运动轨迹制成,M端为抛出点,MN间竖直方向高度差为h.现将一小球套于其上,由静止开始从M端沿杆滑下,已知重力加速度为g,则有( )| A. | 小球做匀变速曲线运动 | |
| B. | 小球从M端运动到N端所需时间等于$\sqrt{\frac{2h}{g}}$ | |
| C. | 运动到N端时,小球速度的水平分量等于$\frac{{v}_{0}\sqrt{2gh}}{\sqrt{2gh+{{v}_{0}}^{2}}}$ | |
| D. | 运动到N端时,小球速度的竖直分量等于$\sqrt{2gh}$ |
| A. | 已知万有引力常量、飞船的圆轨道半径和周期,可以算出地球的质量 | |
| B. | 神舟十号在地面的发射速度应大于11.2 km/s(第二宇宙速度) | |
| C. | 飞船内的宇航员处于失重状态是由于没有受到万有引力的作用 | |
| D. | 飞船的圆轨道半径越大,其线速度越大,周期越大 |
 如图所示,一质量为m=2kg的物体,在水平恒力F的作用下,从静止开始运动,已知F=20N,物体与水平面间的动摩擦因数μ=0.5,g=10m/s2,求:
如图所示,一质量为m=2kg的物体,在水平恒力F的作用下,从静止开始运动,已知F=20N,物体与水平面间的动摩擦因数μ=0.5,g=10m/s2,求: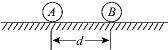 如图:两个带同种电荷的小球A和B,A、B的质量分别为m和2m,开始时将它们固定在绝缘的光滑水平面上保持静止,A、B相距为d,A、B间的相互作用力遵守牛顿第三定律,现同时释放A、B,经过一段时间,B的速度大小为v,A、B间距离为2d.
如图:两个带同种电荷的小球A和B,A、B的质量分别为m和2m,开始时将它们固定在绝缘的光滑水平面上保持静止,A、B相距为d,A、B间的相互作用力遵守牛顿第三定律,现同时释放A、B,经过一段时间,B的速度大小为v,A、B间距离为2d.