题目内容
14.质量分别为M和m的物块形状、大小均相同,将他们通过轻绳和光滑定滑轮连接,如图甲所示,绳子在各处均平行于倾角为α的斜面,M恰好能静止在斜面上,不考虑M、m与斜面之间的摩擦.若互换两物块位置,按图乙放置,然后释放M,斜面仍保持静止,则轻绳的拉力为( )
| A. | Mg | B. | mg | C. | mgsinα | D. | (m+M)gsinα |
分析 由第一次放置M恰好能静止在斜面上,可得M和m的质量关系,进而可求第二次放置M的加速度,轻绳的拉力.
解答 解:第一次放置时M静止,则:
Mgsinα=mg,
第二次放置时候,对整体由牛顿第二定律:
Mg-mgsinα=(M+m)a,
联立解得:a=(1-sinα)g=$\frac{M-m}{M}$g.
对M由牛顿第二定律:
T-mgsinα=ma,
解得:T=mg,
故B正确;
故选:B.
点评 该题的关键是用好牛顿第二定律,对给定的情形分别列方程,同时注意连接体问题的处理方法:整体法和隔离法的灵活应用.

练习册系列答案
相关题目
19.如图所示是某物体运动的v-t图象.下列说法正确的是( )
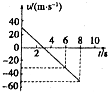

| A. | 该物体的加速度一直不变 | B. | 3s末物体加速度开始改变 | ||
| C. | 0-8s物体一直做匀减速运动 | D. | t=0时和t=6s时物体的速率相等 |
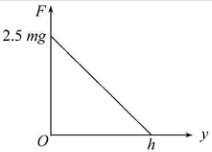 伦敦奥运会女子10米(即跳台距水面10m)跳台比赛中,我国小将陈若琳技压群芳夺得冠军,设陈的质量为m=60kg,其体形可等效为长度l=1.0m,直径d=0.3m的圆柱体,不计空气阻力,当她跳起到达最高点时,她的重心离跳台台面的高度为0.70m,在从起跳到接触水面过程中完成一系列动作,入水后水的等效阻力F(不包括浮力)作用于圆柱体的下端面,F的数值随入水深度y变化的函数图象如图所示,该直线与F轴相交于F=2.5mg处,与y轴相交于y=h(某一未知深度)处,为了确保运动员的安全,水池必须有一定的深度,已知水的密度ρ=1×103kg/m3,g取10m/s2,根据以上数据估算:
伦敦奥运会女子10米(即跳台距水面10m)跳台比赛中,我国小将陈若琳技压群芳夺得冠军,设陈的质量为m=60kg,其体形可等效为长度l=1.0m,直径d=0.3m的圆柱体,不计空气阻力,当她跳起到达最高点时,她的重心离跳台台面的高度为0.70m,在从起跳到接触水面过程中完成一系列动作,入水后水的等效阻力F(不包括浮力)作用于圆柱体的下端面,F的数值随入水深度y变化的函数图象如图所示,该直线与F轴相交于F=2.5mg处,与y轴相交于y=h(某一未知深度)处,为了确保运动员的安全,水池必须有一定的深度,已知水的密度ρ=1×103kg/m3,g取10m/s2,根据以上数据估算: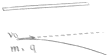 如图,一重力不计的带电粒子以平行于模板的初速度v0从两板正中沿水平方向进入匀强电场,恰好从下极板边缘飞出电场,已知模板长度为L,间距为d,板间电压为U,求粒子的电荷和离开电场时速度方向?
如图,一重力不计的带电粒子以平行于模板的初速度v0从两板正中沿水平方向进入匀强电场,恰好从下极板边缘飞出电场,已知模板长度为L,间距为d,板间电压为U,求粒子的电荷和离开电场时速度方向?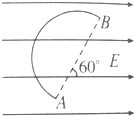 如图所示,带电荷量为-5×10-3C的点电荷在匀强电场中沿半径为10cm的半圆弧由A点运动到B点.已知电场强度E=1.0×103V/m,则此过程中电荷的电势能将如何变化?变化多大?
如图所示,带电荷量为-5×10-3C的点电荷在匀强电场中沿半径为10cm的半圆弧由A点运动到B点.已知电场强度E=1.0×103V/m,则此过程中电荷的电势能将如何变化?变化多大? 如图所示电路中,电阻R1=9Ω,R2=15Ω,电源电动势E=12v,内阻r=1Ω.求
如图所示电路中,电阻R1=9Ω,R2=15Ω,电源电动势E=12v,内阻r=1Ω.求