题目内容
5.在一列沿水平直线传播的简谐横波上有相距4m的A、B两点,如图(甲)、(乙)分别是A、B两质点的振动图象,已知该波波长大于2m,求这列波可能的波速.
分析 由振动图象读出周期.根据同一时刻AB两质点的振动状态,得到AB间的距离与波长的关系,求出波长的通项,根据条件:波长大于2m,得到波长的值,再求解波速的通项.
解答 解:由振动图象得质点振动周期T=0.4 s,
若波由A向B传播,B点比A点晚振动的时间△t=nT+$\frac{3}{4}$T(n=0,1,2,3,…),
所以A、B间的距离为△s=nλ+$\frac{3}{4}λ$(n=0,1,2,3,…),则波长为λ=$\frac{4△s}{4n+3}$=$\frac{16}{4n+3}$,
因为λ>2 m,所以n=0,1,当n=0时,λ1=$\frac{16}{3}$m,v1=$\frac{{λ}_{1}}{{T}_{\;}}=\frac{40}{3}$m/s,当n=1时,λ2=$\frac{16}{7}$m,v2=$\frac{{λ}_{2}}{{T}_{\;}}=\frac{40}{7}$m/s.
若波由B向A传播,A点比B点晚振动的时间△t=nT+$\frac{1}{4}$T(n=0,1,2,3,…),
所以A、B间的距离为△s=nλ+$\frac{1}{4}$λ(n=0,1,2,3,…),则波长为λ=$\frac{4△s}{4n+1}=\frac{16}{4n+1}$
λ>2 m,所以n=0,1,当n=0时,λ1=16m,v1=40m/s,当n=1时,λ2=3.2m,v2=8m/s.
答:这列波可能的波速为$\frac{40}{3}m/s$、$\frac{40}{7}m/s$、40m/s、8m/s.
点评 知道两个质点的振动图象,读出同一时刻质点的位置和速度关系,分析它们状态的关系,画出波形,研究质点间距离与波长的关系,是常规的思路,多做相关训练,有助于强化质点的振动与波动关系.

 名校课堂系列答案
名校课堂系列答案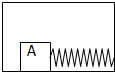 如图所示,在原来静止的木箱内,放有A物体,A物体被伸长的弹簧拉住且静止.现发现物体A被拉动,木箱的运动情况可能是( )
如图所示,在原来静止的木箱内,放有A物体,A物体被伸长的弹簧拉住且静止.现发现物体A被拉动,木箱的运动情况可能是( )| A. | 加速下降 | B. | 减速上升 | C. | 匀速向右运动 | D. | 加速向左运动 |
 如图所示,一个人站在水平地面上的长木板上用力F向右推箱子、木板、人、箱子均处于静止状态,三者的质量均为m,重力加速度为g.下列说法正确的是( )
如图所示,一个人站在水平地面上的长木板上用力F向右推箱子、木板、人、箱子均处于静止状态,三者的质量均为m,重力加速度为g.下列说法正确的是( )| A. | 箱子受到的摩擦力方向向右 | |
| B. | 人受到的摩擦力方向向右 | |
| C. | 地面对木板的摩擦力方向向右 | |
| D. | 若人用斜向下的力推箱子,则木板对地面的压力会大于3mg |
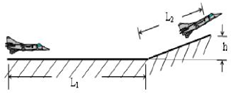 2012年11月23日上午,由来自东海舰队“海空雄鹰团”的飞行员戴明盟驾驶的中国航母舰载机歼-15降落在辽宁舰甲板上,首降成功,随后舰载机通过滑跃式起飞成功,滑跃式起飞有点像高山滑雪,主要靠甲板前端的上翘来帮助战斗机起飞,其示意图如图所示,设某航母起飞跑道主要由长度为L1=160m的水平跑道和长度为L2=20m的倾斜跑道两部分组成,水平跑道与倾斜跑道末端的高度差h=4.0m,一架质量为m=2.0×104kg的飞机,其喷气发动机的推力大小恒定为F=1.2×104N,方向与速度方向相同,在运动过程中飞机受到的平均阻力大小为飞机重力的0.1倍,假设航母处于静止状态,飞机质量视为不变并可看成质点,倾斜跑道看做斜面,不计拐角处的影响,取g=10m/s2
2012年11月23日上午,由来自东海舰队“海空雄鹰团”的飞行员戴明盟驾驶的中国航母舰载机歼-15降落在辽宁舰甲板上,首降成功,随后舰载机通过滑跃式起飞成功,滑跃式起飞有点像高山滑雪,主要靠甲板前端的上翘来帮助战斗机起飞,其示意图如图所示,设某航母起飞跑道主要由长度为L1=160m的水平跑道和长度为L2=20m的倾斜跑道两部分组成,水平跑道与倾斜跑道末端的高度差h=4.0m,一架质量为m=2.0×104kg的飞机,其喷气发动机的推力大小恒定为F=1.2×104N,方向与速度方向相同,在运动过程中飞机受到的平均阻力大小为飞机重力的0.1倍,假设航母处于静止状态,飞机质量视为不变并可看成质点,倾斜跑道看做斜面,不计拐角处的影响,取g=10m/s2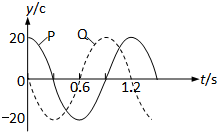 在一列横波的传播方向上有两点P和Q,两点间距离PQ=24m,它们的振动图象如图所示,P点距波源近.
在一列横波的传播方向上有两点P和Q,两点间距离PQ=24m,它们的振动图象如图所示,P点距波源近. m1和m2两物体原来静止,m2物体的夹角为θ,现在施水平力恒力F于物体m1上,若物体与墙、物体与地面之间的摩擦都不计,求两物体运动的加速度各为多大?
m1和m2两物体原来静止,m2物体的夹角为θ,现在施水平力恒力F于物体m1上,若物体与墙、物体与地面之间的摩擦都不计,求两物体运动的加速度各为多大? (1)用多用表的欧姆挡测量阻值约为几十kΩ的电阻Rx,以下给出的是可能的操作步骤,其中S为选择开关,P为欧姆挡调零旋钮,把你认为正确的步骤前的字母按合理的顺序填写在下面的横线上.
(1)用多用表的欧姆挡测量阻值约为几十kΩ的电阻Rx,以下给出的是可能的操作步骤,其中S为选择开关,P为欧姆挡调零旋钮,把你认为正确的步骤前的字母按合理的顺序填写在下面的横线上.