题目内容
一个物体沿着如图所示的固定斜面，自由地向下作匀减速直线运动，在经过A点时的动能为60J，到达B点时恰好静止下来．已知该物体经过这一过程（AB），其机械能减少了80J．要想使得该物体自B点开始，沿着该斜面自由地向正上方，作匀减速运动，到达A点时又恰好能够停下来，那么，该物体在B点时的初动能应该是多大？分析：在该过程中，克服摩擦力做功等于机械能的减小量，通过机械能等于动能和重力势能之和求出AB两点的重力势能之差，从而根据功能关系求出B点的初动能．
解答：解：由摩擦力做功的特点和功能关系知：
物体经过A→B（或B→A）的过程，物体克服滑动摩擦力做功为：
Wf=△E=80J
由功能关系知，物体在A、B两个状态的势能差为：80-60=20J
物体在B点时的动能在过程中消耗去向有两个：
①通过物体克服滑动摩擦力做功的形式转化成了热能80J；
②通过物体克服重力做功的形式转化成了物体的势能20J．
所以，物体在B点时的初动能应该是：80+20=100J．
答：物体在B点的初动能为100J．
物体经过A→B（或B→A）的过程，物体克服滑动摩擦力做功为：
Wf=△E=80J
由功能关系知，物体在A、B两个状态的势能差为：80-60=20J
物体在B点时的动能在过程中消耗去向有两个：
①通过物体克服滑动摩擦力做功的形式转化成了热能80J；
②通过物体克服重力做功的形式转化成了物体的势能20J．
所以，物体在B点时的初动能应该是：80+20=100J．
答：物体在B点的初动能为100J．
点评：本题考查了功能关系，以及能量守恒的综合运用，难度中等，需加强这方面的训练．
练习册系列答案
相关题目
（2011?安徽模拟）如图所示，斜面小车M静止在光滑水平面上，小车左边紧贴墙壁，若在小车斜面上放着一个物体m，当m沿着小车的斜表面下滑时，小车M始终静止不动，则小车M受力个数可能为（ ）
（2011?江苏模拟）如图所示，以O为原点建立直角坐标系Oxy，绝缘光滑水平面沿着x轴，y轴在竖直方向．在水平面上方存在与x轴平行的匀强电场．一个质量m=2.0×10-3kg、电量q=2.0×10-6C的带正电的物体（可作为质点），从O点开始以一定的初速度沿着x轴正方向做直线运动，其位移随时间的变化规律为x=8.0t-10t2，式中x的单位为m，t的单位为s．不计空气阻力，取g=10m/s2．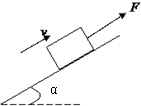
如图所示，一个质量为m的物体，在平行于斜面的拉力F作用下，沿着倾角α的斜面匀速向上运动，已知物体与斜面间的动摩擦因数为μ．求拉力F的大小．