题目内容
7.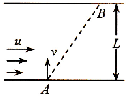 如图所示,河道宽L=200m,越到河中央河水的流速越大,且流速大小满足u=0.2x(x是离河岸的距离,0≤x≤$\frac{L}{2}$ ).一小船在静水中的速度v=10m/s,自A处出发,船头垂直河岸方向渡河到达对岸B处.设船的运动方向与水流方向夹角为θ,下列说法正确的是( )
如图所示,河道宽L=200m,越到河中央河水的流速越大,且流速大小满足u=0.2x(x是离河岸的距离,0≤x≤$\frac{L}{2}$ ).一小船在静水中的速度v=10m/s,自A处出发,船头垂直河岸方向渡河到达对岸B处.设船的运动方向与水流方向夹角为θ,下列说法正确的是( )| A. | 小船渡河时间大于20s | |
| B. | AB两点间距离为 200$\sqrt{2}$m | |
| C. | 到达河中央前小船加速度大小为0.2 m/s2 | |
| D. | 在河中央时θ最小,且tanθ=0.5 |
分析 将船的运动分解为沿河岸方向和垂直于河岸方向,在垂直于河岸方向上的速度等于静水速,根据河宽以及在垂直于河岸方向上的速度求出渡河的时间.水流速与到河岸的最短距离x成正比,是成线性变化的,知水流速的平均速度等于$\frac{d}{4}$处的水流速.根据平均水流速,求出沿河岸方向上的位移,从而求出AB的直线距离,最后根据水流速度与距离的关系,得出在河中央处,水流速度,再结合三角知识,即可求解夹角的最小值.
解答 解:A、渡河的时间t=$\frac{d}{{v}_{c}}$=$\frac{200}{10}$s=20s,故A错误.
B、水流速的平均速度等于$\frac{d}{4}$处的水流速.则有:u=0.2×$\frac{d}{4}$=10m/s.
所以沿河岸方向上的位移为:x=ut=200m.
所以AB的直线距离为:s=$\sqrt{20{0}^{2}+20{0}^{2}}$m=200$\sqrt{2}$m,故B正确;
C、船在静水中速度是不变,而水流速度满足u=0.2x(x是离河岸的距离,0≤x≤$\frac{L}{2}$),因x=vt,那么u=2t,因此到达河中央前小船加速度大小为2 m/s2,故C错误;
D、当到达中央时,水流速度为u=0.2x=0.2×100=20m/s,由三角知识,则有tanθ=$\frac{10}{20}$=0.5,故D正确;
故选:BD.
点评 解决本题的关键知道合运动与分运动具有等时性,各分运动具有独立性,互不影响.同时掌握运动学公式的应用.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
17.直流电动机所加电压为U,测得通过电动机的电流强度为I,已知电动机线圈内阻为r,下列说法正确的是( )
| A. | 电动机消耗的功率为$\frac{{U}^{2}}{r}$ | |
| B. | 电动机消耗的功率为UI | |
| C. | 电动机转化为机械能的功率为UI-I2r | |
| D. | 电动机的发热功率为I2r |
18.为维护消费者权益,某技术监督部门对市场上的电线产品进行抽查,发现有一个品牌的铜芯电线不符合规格:电线直径明显比说明书上标有的直径要小,引起这种电线不符合规格的主要原因是( )
| A. | 电线的长度引起电阻偏大 | B. | 电线的横截面积引起电阻偏大 | ||
| C. | 电线的材料引起电阻偏大 | D. | 电线的温度引起电阻偏大 |
2.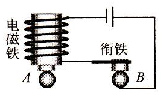 用图示装置探究平抛运动的规律.两个相同的小钢球A、B球心等高,用力向左击打B,使B离开装置做平抛运动,同时电路断开,A自由下落,经一段时间后两球在空中相撞.下列说法正确的是( )
用图示装置探究平抛运动的规律.两个相同的小钢球A、B球心等高,用力向左击打B,使B离开装置做平抛运动,同时电路断开,A自由下落,经一段时间后两球在空中相撞.下列说法正确的是( )
 用图示装置探究平抛运动的规律.两个相同的小钢球A、B球心等高,用力向左击打B,使B离开装置做平抛运动,同时电路断开,A自由下落,经一段时间后两球在空中相撞.下列说法正确的是( )
用图示装置探究平抛运动的规律.两个相同的小钢球A、B球心等高,用力向左击打B,使B离开装置做平抛运动,同时电路断开,A自由下落,经一段时间后两球在空中相撞.下列说法正确的是( )| A. | 该实验说明B在水平方向做匀速运动 | |
| B. | 该实验说明B在竖直方向做自由落体运动 | |
| C. | 若加大击打力度,两球可能不相撞 | |
| D. | 若减小击打力度,两球一定不相撞 |
19.在足够高的楼顶上将一物体竖直向上抛出,物体上升的最大高度为15m,不计空气阻力,设楼够高,则物体位移大小为10m时,物体通过的路程可能为( )
| A. | 10 m | B. | 20 m | C. | 30 m | D. | 40 m |
16.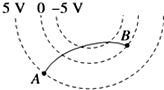 如图所示,虚线表示某电场的等势面.一带电粒子仅在电场力作用下由A运动到B的径迹如图中实线所示.粒子在A点的加速度为aA、电势能为EA;在B点的加速度为aB、电势能为EB.则下列结论正确的是( )
如图所示,虚线表示某电场的等势面.一带电粒子仅在电场力作用下由A运动到B的径迹如图中实线所示.粒子在A点的加速度为aA、电势能为EA;在B点的加速度为aB、电势能为EB.则下列结论正确的是( )
 如图所示,虚线表示某电场的等势面.一带电粒子仅在电场力作用下由A运动到B的径迹如图中实线所示.粒子在A点的加速度为aA、电势能为EA;在B点的加速度为aB、电势能为EB.则下列结论正确的是( )
如图所示,虚线表示某电场的等势面.一带电粒子仅在电场力作用下由A运动到B的径迹如图中实线所示.粒子在A点的加速度为aA、电势能为EA;在B点的加速度为aB、电势能为EB.则下列结论正确的是( )| A. | 粒子带正电,aA>aB,EA>EB | B. | 粒子带负电,aA>aB,EA<EB | ||
| C. | 粒子带正电,aA<aB,EA>EB | D. | 粒子带负电,aA<aB,EA<EB |
1.太阳系中的第二大行星--土星的卫星众多,目前已发现有数十颗.下表是有关土卫五和土卫六两颗卫星的一些参数,则两卫星相比较,下列判断正确的是( )
| 卫星 | 距土星的距离km | 半径/km | 质量/kg | 发现者 | 发现日期 |
| 土卫五 | 527000 | 765 | 2.49×1021 | 卡西尼 | 1672 |
| 土卫六 | 1222000 | 2575 | 1.35×1023 | 惠更斯 | 1655 |
| A. | 土卫五的公转周期更大 | B. | 土星对土卫六的万有引力更大 | ||
| C. | 土卫五的公转角速度大 | D. | 土卫六的公转线速度大 |
 测量电源E的电动势E及内阻r(E约为4.5V,r约为1.5Ω).器材:量程3V内阻为RV=20kΩ的电压表
测量电源E的电动势E及内阻r(E约为4.5V,r约为1.5Ω).器材:量程3V内阻为RV=20kΩ的电压表 ,量程0.5A的电流表具有一定内阻),固定电阻R=18kΩ,滑线变阻器R′=10Ω,电键K,导线若干.
,量程0.5A的电流表具有一定内阻),固定电阻R=18kΩ,滑线变阻器R′=10Ω,电键K,导线若干.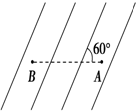 如图所示为一组未知方向的匀强电场的电场线,将带电荷量为q=-1.0×10-6C的点电荷由A点沿水平线移至B点,克服电场力做了2×10-6J的功,已知A、B间的距离为2cm.试求:
如图所示为一组未知方向的匀强电场的电场线,将带电荷量为q=-1.0×10-6C的点电荷由A点沿水平线移至B点,克服电场力做了2×10-6J的功,已知A、B间的距离为2cm.试求: