题目内容
6. 如图所示,半径为r的圆形空间内存在着垂直于纸面向外的匀强磁场,一个带电粒子(不计重力)从A点以速度v0垂直于磁场方向射入磁场中,并由B点射出,且∠AOB=120°,则该粒子在磁场中运动的时间为( )
如图所示,半径为r的圆形空间内存在着垂直于纸面向外的匀强磁场,一个带电粒子(不计重力)从A点以速度v0垂直于磁场方向射入磁场中,并由B点射出,且∠AOB=120°,则该粒子在磁场中运动的时间为( )| A. | $\frac{2πr}{3{v}_{0}}$ | B. | $\frac{2\sqrt{3}πr}{3{v}_{0}}$ | C. | $\frac{πr}{3{v}_{0}}$ | D. | $\frac{\sqrt{3}πr}{3{v}_{0}}$ |
分析 带电粒子在磁场中做匀速圆周运动,由几何关系可求出圆心角和半径,则可求得粒子转过的弧长,由线速度的定义可求得运动的时间.
解答 解:由图可知,粒子转过的圆心角为60°,R=$\sqrt{3}$r; 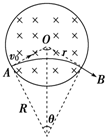
转过的弧长为l=$\frac{60°}{360°}$×2πR=$\frac{πR}{3}$=$\frac{\sqrt{3}πr}{3}$;
则运动所用时间t=$\frac{l}{{v}_{0}}$=$\frac{\sqrt{3}πr}{3{v}_{0}}$;
故选:D.
点评 本题很多同学只想到了用周期来求时间,其实用线速度的定义来求时间也是一个不错的选择.

练习册系列答案
相关题目
17. 如图所示,在半径为R的圆形区域内有匀强磁场.在边长为2R的正方形区域里也有匀强磁场,两个磁场的磁感应强度大小相同.两个相同的带电粒子以相同的速率分别从M、N两点射入匀强磁场.在M点射入的带电粒子,其速度方向指向圆心;在N点射入的带电粒子,速度方向与边界垂直,且N点为正方形边长的中点,则下列说法正确的是( )
如图所示,在半径为R的圆形区域内有匀强磁场.在边长为2R的正方形区域里也有匀强磁场,两个磁场的磁感应强度大小相同.两个相同的带电粒子以相同的速率分别从M、N两点射入匀强磁场.在M点射入的带电粒子,其速度方向指向圆心;在N点射入的带电粒子,速度方向与边界垂直,且N点为正方形边长的中点,则下列说法正确的是( )
 如图所示,在半径为R的圆形区域内有匀强磁场.在边长为2R的正方形区域里也有匀强磁场,两个磁场的磁感应强度大小相同.两个相同的带电粒子以相同的速率分别从M、N两点射入匀强磁场.在M点射入的带电粒子,其速度方向指向圆心;在N点射入的带电粒子,速度方向与边界垂直,且N点为正方形边长的中点,则下列说法正确的是( )
如图所示,在半径为R的圆形区域内有匀强磁场.在边长为2R的正方形区域里也有匀强磁场,两个磁场的磁感应强度大小相同.两个相同的带电粒子以相同的速率分别从M、N两点射入匀强磁场.在M点射入的带电粒子,其速度方向指向圆心;在N点射入的带电粒子,速度方向与边界垂直,且N点为正方形边长的中点,则下列说法正确的是( )| A. | 带电粒子在磁场中飞行的时间不可能相同 | |
| B. | 从N点射入的带电粒子不可能先飞出磁场 | |
| C. | 从M点射入的带电粒子不可能先飞出磁场 | |
| D. | 从N点射入的带电粒子可能比M点射入的带电粒子先飞出磁场 |
14.从某点先后由静止释放金属小球A和B,不计空气阻力.若以B球为参照物,A球的运动是( )
| A. | 匀加速直线运动 | B. | 匀速直线运动 | C. | 静止 | D. | 变加速直线运动 |
1.人造卫星以地心为圆心,做匀速圆周运动,关于其各物理量间的关系,下面说法正确的是( )
| A. | 半径越大,速度越小,周期越小 | |
| B. | 半径越大,速度越小,周期越大 | |
| C. | 所有卫星的线速度均是相同的,与半径无关 | |
| D. | 所有卫星的角速度均是相同的,与半径无关 |
18. 如图所示,一个质量为m的小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.下列中说法正确的是( )
如图所示,一个质量为m的小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.下列中说法正确的是( )
 如图所示,一个质量为m的小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.下列中说法正确的是( )
如图所示,一个质量为m的小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力.下列中说法正确的是( )| A. | 小球运动到半圆弧最高点P时向心力为零 | |
| B. | 小球落到地面前的瞬时其动能为$\frac{5mgR}{2}$ | |
| C. | 小球落地点离p点的水平距离为2$\sqrt{2}$R | |
| D. | 若将半圆弧轨道上部的圆弧截去,其他条件不变,则小球能达到的最大高度比P点高0.5R |
16.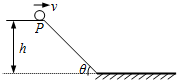 如图所示,一高度为h的光滑水平面与一倾角为θ的斜面连接,一小球以速度v从平面的右端P点向右水平抛出.则小球在空中运动的时间( )
如图所示,一高度为h的光滑水平面与一倾角为θ的斜面连接,一小球以速度v从平面的右端P点向右水平抛出.则小球在空中运动的时间( )
 如图所示,一高度为h的光滑水平面与一倾角为θ的斜面连接,一小球以速度v从平面的右端P点向右水平抛出.则小球在空中运动的时间( )
如图所示,一高度为h的光滑水平面与一倾角为θ的斜面连接,一小球以速度v从平面的右端P点向右水平抛出.则小球在空中运动的时间( )| A. | 一定与v的大小有关 | B. | 一定与v的大小无关 | ||
| C. | 当v足够大时,t与v无关 | D. | 当v足够小时,t与v无关 |
 当金属的温度升高到一定程度时就会向四周发射电子,这种电子叫热电子.通常情况下,热电子的初速度可以忽略不计.如图,相距为L的两平行金属板之间接上高压电源E2,E2的电压恒定为U.电源E1是用来给灯丝加热而产生热电子的,灯丝与M板靠得很近(M、N之间可当作匀强电场).a、b、c、d是匀强电场中的四个均匀分布的等势面.当电源接通后,电流表的示数为I,且保持不变.已知热电子的质量是m、电量是e.求:
当金属的温度升高到一定程度时就会向四周发射电子,这种电子叫热电子.通常情况下,热电子的初速度可以忽略不计.如图,相距为L的两平行金属板之间接上高压电源E2,E2的电压恒定为U.电源E1是用来给灯丝加热而产生热电子的,灯丝与M板靠得很近(M、N之间可当作匀强电场).a、b、c、d是匀强电场中的四个均匀分布的等势面.当电源接通后,电流表的示数为I,且保持不变.已知热电子的质量是m、电量是e.求: