题目内容
如图6—8(a)所示,跨过定滑轮的轻绳两端的物体A和B的质量分别为M和m,物体A 在水平面上。A由静止释放,当B沿竖直方向下落h时,测得A沿水平面运动的速度为v,这时细绳与水平面的夹角为θ,试分析计算B下降h过程中,地面摩擦力对A做的功?(滑轮的质量和摩擦均不计)

mgh-MV2/2-m(Vcosθ)2/2
把物体A、B看成一个整体,对该系统进行受力分析。B下降过程中,B的重力做正功mgh,摩擦力对A做负功,设为Wf。由于A与水平面间的正压力是变化的,又不知动摩擦因数、Wf不能用功的定义求得,只能通过动能定理来求解Wf。1.A的实际运动沿速度v的方向,它可以分解为分别是沿绳方向和绕滑轮转动两个分运动;2.根据第1步的分析和平行四边形法则,画出如图b的矢量图;3.由图(b)中可知,V1为绳的速度,也就是该时刻物体B的瞬时速度,V1=Vcosθ。对系统列动能定理表达式: mgh-Wf=MV2/2+mV12/2,可得Wf=mgh-MV2/2-m(Vcosθ)2/2 。

练习册系列答案
相关题目










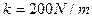 的轻弹簧相连。现用手水平拉弹簧,拉力的作用点移动
的轻弹簧相连。现用手水平拉弹簧,拉力的作用点移动 时,木块开始运动,继续拉弹簧,木块缓慢移动了
时,木块开始运动,继续拉弹簧,木块缓慢移动了 的位移,求上述过程中拉力所做的功。
的位移,求上述过程中拉力所做的功。
