题目内容
17.一颗人造地球卫星离地面高h=3R(R为地球的半径).若已知地地球表面的重力加速度为g,则卫星做匀速圆周运动的速度是$\frac{1}{2}$$\sqrt{gR}$,若已知地球的质量为M,万有引力常量为G,则卫星做匀速圆周运动的角速度是$\frac{1}{8}$$\sqrt{\frac{GM}{{R}^{3}}}$,周期是16π$\sqrt{\frac{{R}^{3}}{GM}}$.分析 人造地球卫星绕地球做匀速圆周运动,根据人造卫星的万有引力等于向心力,列式求出线速度、周期和向心力的表达式,再结合地球表面重力加速度的公式进行讨论即可.
解答 解:人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,有
$\frac{GMm}{{r}^{2}}$=mω2r=m$\frac{{v}^{2}}{r}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
r=4R,
根据万有引力等于重力得地球表面重力加速度为:g=$\frac{GM}{{R}^{2}}$,
若已知地地球表面的重力加速度为g,则卫星做匀速圆周运动的速度是v=$\sqrt{\frac{GM}{r}}$=$\frac{1}{2}$$\sqrt{gR}$,
若已知地球的质量为M,万有引力常量为G,
则卫星做匀速圆周运动的角速度是ω=$\sqrt{\frac{GM}{{r}^{3}}}$=$\frac{1}{8}$$\sqrt{\frac{GM}{{R}^{3}}}$,
周期是T=2π$\sqrt{\frac{{r}^{3}}{GM}}$=16π$\sqrt{\frac{{R}^{3}}{GM}}$,
故答案为:$\frac{1}{2}$$\sqrt{gR}$,$\frac{1}{8}$$\sqrt{\frac{GM}{{R}^{3}}}$,16π$\sqrt{\frac{{R}^{3}}{GM}}$.
点评 本题关键根据人造卫星的万有引力等于向心力,以及地球表面重力等于万有引力列两个方程求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7. 人用手托着质量为m的小苹果,从静止开始沿水平方向运动,前进距离l后,速度为v(小苹果与手始终相对静止),小苹果与手掌之间的动摩擦因数为μ,则下列说法正确的是( )
人用手托着质量为m的小苹果,从静止开始沿水平方向运动,前进距离l后,速度为v(小苹果与手始终相对静止),小苹果与手掌之间的动摩擦因数为μ,则下列说法正确的是( )
 人用手托着质量为m的小苹果,从静止开始沿水平方向运动,前进距离l后,速度为v(小苹果与手始终相对静止),小苹果与手掌之间的动摩擦因数为μ,则下列说法正确的是( )
人用手托着质量为m的小苹果,从静止开始沿水平方向运动,前进距离l后,速度为v(小苹果与手始终相对静止),小苹果与手掌之间的动摩擦因数为μ,则下列说法正确的是( )| A. | 手对小苹果的作用力方向始终竖直向上 | |
| B. | 小苹果所受摩擦力大小为μmg | |
| C. | 手对小苹果做的功为$\frac{1}{2}$mv2 | |
| D. | 速度为v时,小苹果重力的瞬时功率为mgv |
8.关于机械振动和机械波下列叙述正确的是( )
| A. | 机械波不是传播能量的一种方式 | |
| B. | 振动质点的频率随着波的传播而减小 | |
| C. | 在波的传播过程中,振动质点和运动形式一起传播 | |
| D. | 在波的传播中,如振源停止振动,波的传播并不会立即停止 |
5.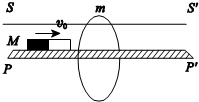 如图所示,一根足够长的水平滑杆SS′上套有一质量为m的光滑金属圆环,在滑杆的正下方与其平行放置一足够长的光滑水平的绝缘轨道PP′,PP′穿过金属环的圆心.现使质量为M的条形磁铁以水平速度v0沿绝缘轨道向右运动,则( )
如图所示,一根足够长的水平滑杆SS′上套有一质量为m的光滑金属圆环,在滑杆的正下方与其平行放置一足够长的光滑水平的绝缘轨道PP′,PP′穿过金属环的圆心.现使质量为M的条形磁铁以水平速度v0沿绝缘轨道向右运动,则( )
 如图所示,一根足够长的水平滑杆SS′上套有一质量为m的光滑金属圆环,在滑杆的正下方与其平行放置一足够长的光滑水平的绝缘轨道PP′,PP′穿过金属环的圆心.现使质量为M的条形磁铁以水平速度v0沿绝缘轨道向右运动,则( )
如图所示,一根足够长的水平滑杆SS′上套有一质量为m的光滑金属圆环,在滑杆的正下方与其平行放置一足够长的光滑水平的绝缘轨道PP′,PP′穿过金属环的圆心.现使质量为M的条形磁铁以水平速度v0沿绝缘轨道向右运动,则( )| A. | 磁铁将不会穿越滑环运动 | |
| B. | 磁铁穿过金属环后,两者最终将相对静止 | |
| C. | 圆环的最终速度为$\frac{{M{v_0}}}{M+m}$ | |
| D. | 整个过程最多能产生热量$\frac{Mmv_0^2}{M+m}$ |
9.下列关于匀速圆周运动的说法中,正确的是( )
| A. | 是线速度不变的运动 | B. | 是相对圆心位移不变的运动 | ||
| C. | 是角速度不断变化的运动 | D. | 是角速度不变的运动 |
6.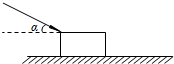 放在水平地面上的物块,受到一个与水平方向成α角斜向下方的力F的作用,物块在水平地面静止,如图所示.如果保持力F的大小不变,而使力F与水平方向的夹角α增大,那么,地面受到的压力N和物块受到的摩擦力f的变化情况是( )
放在水平地面上的物块,受到一个与水平方向成α角斜向下方的力F的作用,物块在水平地面静止,如图所示.如果保持力F的大小不变,而使力F与水平方向的夹角α增大,那么,地面受到的压力N和物块受到的摩擦力f的变化情况是( )
 放在水平地面上的物块,受到一个与水平方向成α角斜向下方的力F的作用,物块在水平地面静止,如图所示.如果保持力F的大小不变,而使力F与水平方向的夹角α增大,那么,地面受到的压力N和物块受到的摩擦力f的变化情况是( )
放在水平地面上的物块,受到一个与水平方向成α角斜向下方的力F的作用,物块在水平地面静止,如图所示.如果保持力F的大小不变,而使力F与水平方向的夹角α增大,那么,地面受到的压力N和物块受到的摩擦力f的变化情况是( )| A. | N变小,f变大 | B. | N变小,f变小 | C. | N变大,f变小 | D. | N变大,f不变 |
3.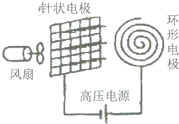 空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5000V左右,使空气发生电离,从而产生一价的负氧离子排出,使空气清新化,针状负极与环形正极间距为5mm,且视为匀强电场,电子电量e=1.60×10-19C;若电场强度为E,电场对负氧离子的作用力为F,则 ( )
空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5000V左右,使空气发生电离,从而产生一价的负氧离子排出,使空气清新化,针状负极与环形正极间距为5mm,且视为匀强电场,电子电量e=1.60×10-19C;若电场强度为E,电场对负氧离子的作用力为F,则 ( )
 空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5000V左右,使空气发生电离,从而产生一价的负氧离子排出,使空气清新化,针状负极与环形正极间距为5mm,且视为匀强电场,电子电量e=1.60×10-19C;若电场强度为E,电场对负氧离子的作用力为F,则 ( )
空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5000V左右,使空气发生电离,从而产生一价的负氧离子排出,使空气清新化,针状负极与环形正极间距为5mm,且视为匀强电场,电子电量e=1.60×10-19C;若电场强度为E,电场对负氧离子的作用力为F,则 ( )| A. | E=1O3N/C,F=1.6×10-l6N | B. | E=106N/C,F=1.6×10-16N | ||
| C. | E=103N/C,F=1.6×10-13N | D. | E=106N/C,F=1.6×l0-13N |
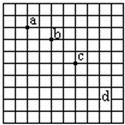 如图所示,在“研究平抛物体运动”的实验中,有一张印有小方格的纸记录轨迹,小方格的边长L=1.25cm.若小球在平抛运动过程中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为v0=2$\sqrt{gL}$(用L、g表示),其值为0.7m/s(g=9.8m/s2),小球在b点的速度为0.88m/s.
如图所示,在“研究平抛物体运动”的实验中,有一张印有小方格的纸记录轨迹,小方格的边长L=1.25cm.若小球在平抛运动过程中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为v0=2$\sqrt{gL}$(用L、g表示),其值为0.7m/s(g=9.8m/s2),小球在b点的速度为0.88m/s.