题目内容
正在粗糙水平面上滑动的物块,从t1时刻到t2时刻受到恒定的水平推力F的作用,在这段时间内物块做直线运动,已知物块在t1时刻的速度与t2时刻的速度大小相等,则在此过程中
- A.物块可能做匀速直线运动
- B.物块的位移可能为零
- C.物块动量的变化一定为零
- D.F一定对物块做正功
AD
分析:物体做直线运动,合力与速度同方向,由于初末速度相等,物体可能做匀速直线运动,也有可能速度先减为零,然后反向增加,根据运动学公式结合牛顿第二定律判断.
解答:A、物体做直线运动,合力与速度同方向,初末速度相等,物体可能做匀速直线运动,即推力等于滑动摩擦力,故A正确;
B、物体有可能速度先减为零,然后反向增加到相同的值,即力F向后,故减速时加速度为a1=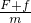 ,加速时加速度为a2=
,加速时加速度为a2=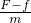 ,根据速度位移公式,减速位移
,根据速度位移公式,减速位移 ,加速位移为
,加速位移为 ,故总位移x=x1-x2≠0,故B错误;
,故总位移x=x1-x2≠0,故B错误;
C、物体可能做匀速直线运动,也有可能速度先减为零,然后反向增加,由于动量为矢量,故动量变化不一定为零,故C错误;
D、物体可能做匀速直线运动,则推力等于滑动摩擦力,一定做正功;
物体也可能先减速前进和加速后退,即力F向后,故减速时加速度为a1=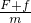 ,加速时加速度为a2=
,加速时加速度为a2=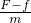 ,根据速度位移公式,减速位移
,根据速度位移公式,减速位移 ,加速位移为
,加速位移为 ,故总位移x=x1-x2<0,即物体后退的位移较大,故力F也一定做正功,故D正确;
,故总位移x=x1-x2<0,即物体后退的位移较大,故力F也一定做正功,故D正确;
故选AD.
点评:本题关键是分匀速直线运动和先减速和反向加速运动两种情况进行分析,对于第二种情况,先根据牛顿第二定律求出加速度,再根据运动学公式判断前进与后退的位移大小,再根据公的定义进行判断.
分析:物体做直线运动,合力与速度同方向,由于初末速度相等,物体可能做匀速直线运动,也有可能速度先减为零,然后反向增加,根据运动学公式结合牛顿第二定律判断.
解答:A、物体做直线运动,合力与速度同方向,初末速度相等,物体可能做匀速直线运动,即推力等于滑动摩擦力,故A正确;
B、物体有可能速度先减为零,然后反向增加到相同的值,即力F向后,故减速时加速度为a1=
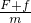 ,加速时加速度为a2=
,加速时加速度为a2=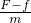 ,根据速度位移公式,减速位移
,根据速度位移公式,减速位移 ,加速位移为
,加速位移为 ,故总位移x=x1-x2≠0,故B错误;
,故总位移x=x1-x2≠0,故B错误;C、物体可能做匀速直线运动,也有可能速度先减为零,然后反向增加,由于动量为矢量,故动量变化不一定为零,故C错误;
D、物体可能做匀速直线运动,则推力等于滑动摩擦力,一定做正功;
物体也可能先减速前进和加速后退,即力F向后,故减速时加速度为a1=
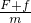 ,加速时加速度为a2=
,加速时加速度为a2=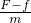 ,根据速度位移公式,减速位移
,根据速度位移公式,减速位移 ,加速位移为
,加速位移为 ,故总位移x=x1-x2<0,即物体后退的位移较大,故力F也一定做正功,故D正确;
,故总位移x=x1-x2<0,即物体后退的位移较大,故力F也一定做正功,故D正确;故选AD.
点评:本题关键是分匀速直线运动和先减速和反向加速运动两种情况进行分析,对于第二种情况,先根据牛顿第二定律求出加速度,再根据运动学公式判断前进与后退的位移大小,再根据公的定义进行判断.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目