题目内容
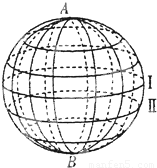
 在2008年中央电视台举办的元宵文艺晚会上,杂技“飞车”演员驾着摩托车,在球形金属网内壁上下盘旋,惊险、刺激,令人惊叹不已,赢得阵阵掌声,如图所示球形金属网的半径为R,假设两杂技运动员(总质量相同)骑摩托车在球形金属网内做“飞车”表演时,以相同的速率分别行驶在Ⅰ、Ⅱ两个水平轨道上,轨道Ⅰ的平面过球形金属网的球心,轨道Ⅱ的平面在轨道Ⅰ平面下方且与轨道Ⅰ的平面间距为h,则( )
在2008年中央电视台举办的元宵文艺晚会上,杂技“飞车”演员驾着摩托车,在球形金属网内壁上下盘旋,惊险、刺激,令人惊叹不已,赢得阵阵掌声,如图所示球形金属网的半径为R,假设两杂技运动员(总质量相同)骑摩托车在球形金属网内做“飞车”表演时,以相同的速率分别行驶在Ⅰ、Ⅱ两个水平轨道上,轨道Ⅰ的平面过球形金属网的球心,轨道Ⅱ的平面在轨道Ⅰ平面下方且与轨道Ⅰ的平面间距为h,则( )分析:根据几何关系求出轨道Ⅱ的轨道半径r,根据周期公式、向心加速度公式列式即可求解.
解答:解:A、由题意得:轨道Ⅰ的轨迹半径为R,根据几何关系可知:轨道Ⅱ的轨道半径r=
,所以轨道Ⅰ与轨道Ⅱ的轨道半径之比为
,故A错误;
B、根据周期公式得:轨道Ⅰ的周期为T=
,轨道Ⅱ上运动的周期为
,所以在轨道Ⅰ与轨道Ⅱ上运动的周期之比为
,故B错误;
C、根据a=
可知:在轨道Ⅰ与轨道Ⅱ上运动的向心加速度之比为
,故C正确;
D、在轨道Ⅰ上,球形金属网对摩托车的压力为N=m
,在轨道Ⅱ上球形金属网对摩托车的压力为N′=
=m
,所以在轨道Ⅰ与轨道Ⅱ上对球形金属网的压力之比为
,故D正确.
故选CD
| R2-h2 |
| R | ||
|
B、根据周期公式得:轨道Ⅰ的周期为T=
| 2πR |
| v |
2π
| ||
| v |
| R | ||
|
C、根据a=
| v2 |
| r |
| ||
| R |
D、在轨道Ⅰ上,球形金属网对摩托车的压力为N=m
| v2 |
| R |
m
| ||
|
| v2R |
| r2 |
| R2-h2 |
| R2 |
故选CD
点评:本题主要考查了向心力公式的直接应用,要求同学们能正确对摩托车进行受力分析,结合几何关系求解,难度适中.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目