题目内容
如图所示,长度为L、倾角θ=30°的斜面AB,在斜面顶端B向左水平抛出小球1、同时在底端A正上方某高度处水平向右抛出小球2,小球2垂直撞在斜面上的位置P,小球1也同时落在P点。求两球平抛的初速度v1、v2和BD间距离h。

0.3L
设运动时间为t、小球1和2的初速度为v1和v2、B球下落高度为h,小球1做平抛运动落在斜面上,有tan θ=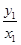 ,(1分)
,(1分)
又x1=v1t,y1=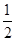 gt2, (2分)
gt2, (2分)
解得tan θ=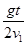 ① (1分)
① (1分)
小球2垂直撞在斜面上,有tan θ=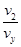 ,即tan θ=
,即tan θ=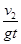 ② (1分)
② (1分)
根据几何关系有x1+x2=Lcos θ,即(v1+v2)t=Lcos θ ③ (2分)
联立①②得v2=2v1tan2θ ④, (1分)
①③联立得2v1(v1+v2)tan θ=gLcos θ ⑤ (2分)
④⑤联立解得v1=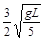 、v2=
、v2=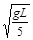 , (2分)
, (2分)
代入③解得t=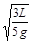 (1分)
(1分)
则下落高度h=y1=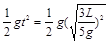 =0.3L. (2分
=0.3L. (2分
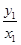 ,(1分)
,(1分)又x1=v1t,y1=
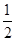 gt2, (2分)
gt2, (2分)解得tan θ=
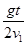 ① (1分)
① (1分)小球2垂直撞在斜面上,有tan θ=
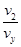 ,即tan θ=
,即tan θ=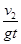 ② (1分)
② (1分)根据几何关系有x1+x2=Lcos θ,即(v1+v2)t=Lcos θ ③ (2分)
联立①②得v2=2v1tan2θ ④, (1分)
①③联立得2v1(v1+v2)tan θ=gLcos θ ⑤ (2分)
④⑤联立解得v1=
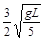 、v2=
、v2=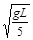 , (2分)
, (2分)代入③解得t=
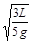 (1分)
(1分)则下落高度h=y1=
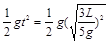 =0.3L. (2分
=0.3L. (2分
练习册系列答案
相关题目
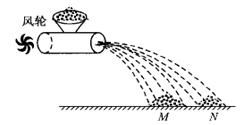


 的斜坡上的A点。已知每块砖的平均厚度为20cm,抛出点到A点竖直方向刚好相距100块砖, (sin370="0.6." cos370=0.8)求:
的斜坡上的A点。已知每块砖的平均厚度为20cm,抛出点到A点竖直方向刚好相距100块砖, (sin370="0.6." cos370=0.8)求:

