题目内容
13.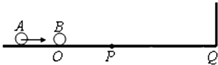 如图所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,Q点处为一竖直的墙壁.小球A与小球B发生弹性碰撞后两小球均向右运动,小球B与墙壁碰撞后原速率返回并与小球A在P点相遇,$\overline{PQ}=2\overline{PO}$,求
如图所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球的前方O点处有一质量为m2的小球B处于静止状态,Q点处为一竖直的墙壁.小球A与小球B发生弹性碰撞后两小球均向右运动,小球B与墙壁碰撞后原速率返回并与小球A在P点相遇,$\overline{PQ}=2\overline{PO}$,求(ⅰ)两小球质量之比m1:m2;
(ⅱ)若m1和v0已知,并假设两小球第一次碰撞的时间是t秒,求两小球第一次碰撞时平均作用力的大小.
分析 根据碰后再次相遇的路程关系,求出小球碰后的速度大小之比,根据碰撞过程中动量、能量守恒列方程即可求出两球的质量之比.通过动量定理求出两小球第一次碰撞时平均作用力的大小.
解答 解:(ⅰ)设A、B两个小球碰撞后的速度分别为v1、v2,由动量守恒定律有:
m1v0=m1v1+m2v2…①
由能量守恒定律有:$\frac{1}{2}{m_1}v_0^2=\frac{1}{2}{m_1}v_1^2+\frac{1}{2}{m_2}v_2^2$…②
两个小球碰撞后到再次相遇,其速度率不变,由运动学规律有:
v1:v2=$\overline{PO}$:($\overline{PO}+2\overline{PQ}$)=1:5…③
联立①②③,代入数据解得:m1:m2=5:3
(ⅱ)以A球为研究对象,由动量定理有:
$-\overline Ft={m_1}{v_1}-{m_1}{v_0}$…④
联立①④,代入数据解得:$\overline F=\frac{{3{m_1}{v_0}}}{4t}$.
答:(ⅰ)两小球质量之比m1:m2为 5:3.
(ⅱ)两小球第一次碰撞时平均作用力的大小为$\frac{3{m}_{1}{v}_{0}}{4t}$.
点评 解答本题的突破口是根据碰后路程关系求出碰后的速度大小之比,本题很好的将直线运动问题与动量守恒和功能关系联系起来,比较全面的考查了基础知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图所示内壁光滑的环形槽半径为R.固定在竖直平面内,质量均为m的小球A、B以等大的速率v0从圆心等高处向上、向下滑入环形槽,若在运动过程中两球均未脱离环形槽,设当地重力加速度为g.则下列叙述正确( )
如图所示内壁光滑的环形槽半径为R.固定在竖直平面内,质量均为m的小球A、B以等大的速率v0从圆心等高处向上、向下滑入环形槽,若在运动过程中两球均未脱离环形槽,设当地重力加速度为g.则下列叙述正确( )
 如图所示内壁光滑的环形槽半径为R.固定在竖直平面内,质量均为m的小球A、B以等大的速率v0从圆心等高处向上、向下滑入环形槽,若在运动过程中两球均未脱离环形槽,设当地重力加速度为g.则下列叙述正确( )
如图所示内壁光滑的环形槽半径为R.固定在竖直平面内,质量均为m的小球A、B以等大的速率v0从圆心等高处向上、向下滑入环形槽,若在运动过程中两球均未脱离环形槽,设当地重力加速度为g.则下列叙述正确( )| A. | 两球再次相遇时,速率仍然相等 | |
| B. | 小球v0的最小值为$\sqrt{2gR}$ | |
| C. | 小球A通过最高点时的机械能小于小球B通过最低点时的机械能 | |
| D. | 小球A通过最高点和小球B通过最低点时对环形槽的压力差值为6mg |
1.电子所带电荷量最早是由美国物理学家密立根测得的,他根据实验中观察到带电油滴悬浮在电场中,即油滴所受电场力和重力平衡,得出油滴的电荷量.某次实验中测得到多个油滴的带电量Q如表(单位10-19C),则下列说法正确的是( )
| 6.41 | 8.01 | 9.65 | 11.23 | 14.48 | 17.66 | 20.62 | … |
| A. | 密立根通过实验发现了电子 | |
| B. | 密立根通过实验证明了电子带负电 | |
| C. | 在实验误差允许范围内,油滴所带电量之差相等 | |
| D. | 在实验误差允许范围内,油滴所带电量是1.6×10-19C的整数倍 |
18. 嫦娥三号”于2013年12月2日在中国西昌卫星发射中心由长征三号乙运载火箭送人太空,12月14日成功软着陆于月球雨海西北部,12月15日完成着陆器和巡视器分离,并陆续开展了“观天、看地、测月”,的科学探测和其它预定任务.如图所示为“嫦娥三号”释放出的国产“玉兔”号月球车,若该月球车在地球表面的重力为G1,在月球表面的重力为G2,已知地球半径为R1,月球半径为R2,地球表面处的重力加速度为g,则( )
嫦娥三号”于2013年12月2日在中国西昌卫星发射中心由长征三号乙运载火箭送人太空,12月14日成功软着陆于月球雨海西北部,12月15日完成着陆器和巡视器分离,并陆续开展了“观天、看地、测月”,的科学探测和其它预定任务.如图所示为“嫦娥三号”释放出的国产“玉兔”号月球车,若该月球车在地球表面的重力为G1,在月球表面的重力为G2,已知地球半径为R1,月球半径为R2,地球表面处的重力加速度为g,则( )
 嫦娥三号”于2013年12月2日在中国西昌卫星发射中心由长征三号乙运载火箭送人太空,12月14日成功软着陆于月球雨海西北部,12月15日完成着陆器和巡视器分离,并陆续开展了“观天、看地、测月”,的科学探测和其它预定任务.如图所示为“嫦娥三号”释放出的国产“玉兔”号月球车,若该月球车在地球表面的重力为G1,在月球表面的重力为G2,已知地球半径为R1,月球半径为R2,地球表面处的重力加速度为g,则( )
嫦娥三号”于2013年12月2日在中国西昌卫星发射中心由长征三号乙运载火箭送人太空,12月14日成功软着陆于月球雨海西北部,12月15日完成着陆器和巡视器分离,并陆续开展了“观天、看地、测月”,的科学探测和其它预定任务.如图所示为“嫦娥三号”释放出的国产“玉兔”号月球车,若该月球车在地球表面的重力为G1,在月球表面的重力为G2,已知地球半径为R1,月球半径为R2,地球表面处的重力加速度为g,则( )| A. | 月球表面处的重力加速度为$\frac{{G}_{2}}{{G}_{1}}$g | |
| B. | 月球车内的物体处于完全失重状态 | |
| C. | 地球的第一宇宙速度与月球的第一宇宙速度之比为$\sqrt{\frac{{G}_{1}{R}_{1}}{{G}_{2}{R}_{2}}}$ | |
| D. | 地球与月球的质量之比为$\frac{{G}_{1}{{R}_{2}}^{2}}{{G}_{2}{{R}_{1}}^{2}}$ |
5.关于电磁波和相对论,下列说法正确的是( )
| A. | 由于高频电磁波向外界辐射能量的本领更强,所以经过调制的高频电磁波才能把我们要发射的信号发射出去 | |
| B. | 电磁波是由恒定的电场和磁场产生的 | |
| C. | 研究高速火车的运动必须利用相对沦的知识 | |
| D. | 研究速度接近于光速的粒子的运动利用相对论的知识 |
2.某时刻,质量为2kg的物体甲受到的合力是6N,速度是10m/s;质量为3kg的物体乙受到的合力是5N,速度是10m/s,则( )
| A. | 甲比乙的惯性小 | B. | 甲比乙的惯性大 | ||
| C. | 甲和乙的惯性一大 | D. | 无法判定哪个物体惯性大 |
3.在电梯匀速上升的过程中,站在电梯里的人( )
| A. | 所受支持力做负功,机械能减少 | B. | 所受支持力做负功,机械能增加 | ||
| C. | 所受支持力做正功,机械能减少 | D. | 所受支持力做正功,机械能增加 |
 一半圆形导体棒,置于如图所示的匀强磁场中,磁场与半圆所在的平面垂直,已知半圆的半径R=10cm,磁场的磁感应强度B=0.10T,棒中通有电流I=2A,则导体棒所受的安培力大小为0.04N,方向水平向右.
一半圆形导体棒,置于如图所示的匀强磁场中,磁场与半圆所在的平面垂直,已知半圆的半径R=10cm,磁场的磁感应强度B=0.10T,棒中通有电流I=2A,则导体棒所受的安培力大小为0.04N,方向水平向右.