题目内容
10.已知质量分布均匀的球壳对其内部物体的引力为零.科学家设想在赤道正上方高d处和正下方深为d处各修建一环形轨道,轨道面与赤道面共面.现有A、B两物体分别在上述两轨道中做匀速圆周运动,若地球半径为R,轨道对它们均无作用力,则A、B两物体运动的说法正确的是( )| A. | 向心加速度大小的比为$\frac{{R}^{3}}{(R+d)^{2}(R-d)}$ | B. | 线速度大小的比为$\frac{R}{{R}^{2}-{d}^{2}}$$\sqrt{R(R+d)}$ | ||
| C. | 角速度的比为$\sqrt{\frac{{R}^{3}}{(R+d)^{3}}}$ | D. | 周期之比为2π$\sqrt{\frac{(R+d)^{3}}{(R-d)^{3}}}$ |
分析 由地球质量等于密度乘以体积,可得地球质量表达式;由万有引力提供向心力,对A、B分别列方程可得两物体速度和加速度之比.
解答 解:设地球密度为ρ,则有:
在赤道上方:$\frac{{Gρ\frac{4}{3}π{R^3}}}{{{{(R+d)}^2}}}=\frac{v_1^2}{R+d}={a_1}=(R+d){ω_1}^2=\frac{{4{π^2}(R+d)}}{{{T_1}^2}}$
在赤道下方:$\frac{{Gρ\frac{4}{3}π{{(R-d)}^3}}}{{{{(R-d)}^2}}}=\frac{v_2^2}{R-d}={a_2}=(R-d){ω_2}^2=\frac{{4{π^2}(R-d)}}{{{T_2}^2}}$
解得:
$\frac{a_1}{a_2}=\frac{R^3}{{{{(R+d)}^2}(R-d)}}$,故A正确;
$\frac{{v}_{1}}{{v}_{2}}$=$\frac{R}{{R}^{2}-{d}^{2}}$$\sqrt{R(R+d)}$,故B正确;
$\frac{ω_1}{ω_2}$=$\sqrt{\frac{{R}^{3}}{{(R+d)}^{3}}}$,故C正确;
$\frac{T_1}{T_2}=\sqrt{\frac{{{{(R+d)}^3}}}{R^3}}$,故D错误;
故选:ABC
点评 本题主要掌握万有引力提供向心力的基本应用,要会用数学方法表示球体质量;并正确应用万有引力充当向心力求解各物理量的表达式.

练习册系列答案
相关题目
20.下列说法正确的是( )
| A. | 物体的速度越小,惯性也越小 | |
| B. | 如果有摩擦力,则其大小一定与弹力成正比 | |
| C. | 形状规则的物体,它的重心一定在几何中心上 | |
| D. | 木块在桌面上受到的向上的弹力,是由于桌面发生微小的形变而产生的 |
5.离太阳最近的恒星是位于半人马座的南门二,我国民间称作“寿星”.现已探明南门二是一个三合星系,其中A星和B星可以看做在两个圆轨道上绕着二者连线的某点作 匀速圆周运动,两星之间距离约为23个天文单位(1个天文单位约合1.5亿公里,为地球到太阳的平均距离),周期约为80年,C星离A、B星构成的系统很远,在距离A、B两星约为13000个天文单位的圆轨道上绕A、B星运动.据此可知,C星的环绕周期约为( )
| A. | 1000年 | B. | 1万年 | C. | 10万年 | D. | 100万年 |
19.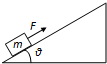 如图所示,倾角为θ的光滑斜面足够长,一物质量为m小物体,在沿斜面向上的恒力F作用下,由静止从斜面底端沿斜面向上做匀加速直线运动,经过时间t,力F做功为60J,此后撤去力F,物体又经过相同的时间t回到斜面底端,若以地面为零势能参考面,则下列说法正确的是( )
如图所示,倾角为θ的光滑斜面足够长,一物质量为m小物体,在沿斜面向上的恒力F作用下,由静止从斜面底端沿斜面向上做匀加速直线运动,经过时间t,力F做功为60J,此后撤去力F,物体又经过相同的时间t回到斜面底端,若以地面为零势能参考面,则下列说法正确的是( )
 如图所示,倾角为θ的光滑斜面足够长,一物质量为m小物体,在沿斜面向上的恒力F作用下,由静止从斜面底端沿斜面向上做匀加速直线运动,经过时间t,力F做功为60J,此后撤去力F,物体又经过相同的时间t回到斜面底端,若以地面为零势能参考面,则下列说法正确的是( )
如图所示,倾角为θ的光滑斜面足够长,一物质量为m小物体,在沿斜面向上的恒力F作用下,由静止从斜面底端沿斜面向上做匀加速直线运动,经过时间t,力F做功为60J,此后撤去力F,物体又经过相同的时间t回到斜面底端,若以地面为零势能参考面,则下列说法正确的是( )| A. | 物体回到斜面底端的动能60J | |
| B. | 恒力F=2mgsinθ | |
| C. | 撤出力F时,物体的重力势是45J | |
| D. | 动能与势能相等的时刻一出现在撤去力F之后 |

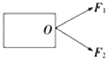 如图所示物体受到大小相等的两个拉力作用,每个拉力都是30N,夹角是60°,求这两个力的合力大小.
如图所示物体受到大小相等的两个拉力作用,每个拉力都是30N,夹角是60°,求这两个力的合力大小.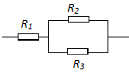 如图所示,R1=4Ω、R2=6Ω、R3=3Ω整个装置接在6V的恒压源上,则
如图所示,R1=4Ω、R2=6Ω、R3=3Ω整个装置接在6V的恒压源上,则