题目内容
【题目】足球比赛中，经常使用“边路突破，下底传中”的战术，即攻方队员带球沿边线前进，到底线附近进行传中．某足球场长90m、宽60m．攻方前锋在中线处将足球沿边线向前踢出，足球的运动可视为在地面上做初速度为l2m/s的匀减速直线运动，加速度大小为2m/s2．试求：
(1)足球从开始做匀减速运动后4s时的速度大小；
(2)足球从开始做匀减速运动后8s时的位移大小；
(3)足球开始做匀减速直线运动的同时，该前锋队员沿边线向前追赶足球．他的启动过程可以视为初速度为0，加速度为2m/s2的匀加速直线运动，他能达到的最大速度为8m/s．该前锋队员至少经过多长时间能追上足球？
【答案】(1)24m(2)36m(3)6.5s
【解析】(1) 
(2)足球速度减为零的时间为
∴8s内的位移为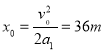
⑶队员达到最大速度的时间为 
队员的位移为
队员匀速至足球停止时的位移为
∴足球停止时队员还未追上，此后
故队员追上足球的时间为
-
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
