题目内容
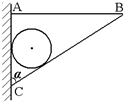 如图所示,球重为G,半径为R,由轻杆BC支持并靠在墙上,轻杆长为L,C端铰于墙上,B端用水平绳拉住,系于墙上A处,杆与墙的夹角为α.
如图所示,球重为G,半径为R,由轻杆BC支持并靠在墙上,轻杆长为L,C端铰于墙上,B端用水平绳拉住,系于墙上A处,杆与墙的夹角为α.
问:(1)球对轻杆的压力为多大?
(2)水平绳的拉力为多大?
(3)若α角可调,则α为多大时水平绳的拉力最小,最小值为多少?
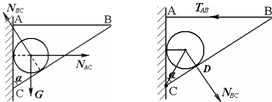 解:(1)、对小球受力分析如图所示;小球受三力而处于平衡状态,则由共点力的平衡条件可知:
解:(1)、对小球受力分析如图所示;小球受三力而处于平衡状态,则由共点力的平衡条件可知:NBC=
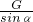
(2)、对BC分析可知,BC以C为轴转动,受AB的拉力及D点的弹力而处于平衡状态;则由力矩平衡条件可知:
NBCDC=TABBCcosα
DC=Rctg(
 )
)联立解得:
TBC=
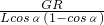
(3)、由数学知识可知:
cosα(1-cosα)≤

当cosα=(1-cosα),即α=60°,即α=60°时绳AB的拉力有最小值:
TBCmin=
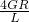
答:(1)球对轻杆的压力为
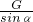 ;(2)水平绳的拉力为
;(2)水平绳的拉力为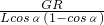 ;(3)当α=60°时拉力最小,最小值为
;(3)当α=60°时拉力最小,最小值为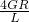 .
.分析:(1)对物体进行受力分析,由共点力的平衡条件可得出轻杆以球的弹力;再由牛顿第三定律可得出球对轻杆的压力;
(2)对BC受力分析,由力矩平衡条件可求得水平绳的拉力为多大;
(3)由(2)中得出的函数关系利用三角函数关系可得出何时拉力最小,最小值为多少.
点评:本题考查共点力的平衡及力矩的平衡条件,注意正确的进行受力分析,并根据平衡条件列出公式进行求解.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图所示,球重为G,半径为R,紧靠在竖直墙上,木块重为W,厚为h,放在球边,当对木块施以水平推力F后,球刚好对地面压力为零,如不计一切摩擦,
如图所示,球重为G,半径为R,紧靠在竖直墙上,木块重为W,厚为h,放在球边,当对木块施以水平推力F后,球刚好对地面压力为零,如不计一切摩擦,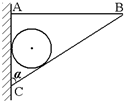 如图所示,球重为G,半径为R,由轻杆BC支持并靠在墙上,轻杆长为L,C端铰于墙上,B端用水平绳拉住,系于墙上A处,杆与墙的夹角为α.
如图所示,球重为G,半径为R,由轻杆BC支持并靠在墙上,轻杆长为L,C端铰于墙上,B端用水平绳拉住,系于墙上A处,杆与墙的夹角为α.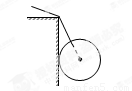
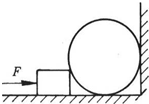 如图所示,球重为G,半径为R,紧靠在竖直墙上,木块重为W,厚为h,放在球边,当对木块施以水平推力F后,球刚好对地面压力为零,如不计一切摩擦,
如图所示,球重为G,半径为R,紧靠在竖直墙上,木块重为W,厚为h,放在球边,当对木块施以水平推力F后,球刚好对地面压力为零,如不计一切摩擦,