题目内容
14. 如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内0点受大小为F的力作用从静止开始做匀加速直线运动,经过t时间质点运动到A点,A、0两点距离为a,在A 点作用力突然变为沿y轴正方向,大小仍为F,再经t时间质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向,下列对运动过程的分析不正确的是( )
如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内0点受大小为F的力作用从静止开始做匀加速直线运动,经过t时间质点运动到A点,A、0两点距离为a,在A 点作用力突然变为沿y轴正方向,大小仍为F,再经t时间质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向,下列对运动过程的分析不正确的是( )| A. | O、B两点距离为 a | |
| B. | C点与x轴的距离为(1+)a | |
| C. | 质点在B点的速度方向与x轴成45° | |
| D. | 质点从O点运动到C点所用时间可能为(1+π)t |
分析 质点从O到A做匀加速直线运动,从A到B做类平抛运动,从B到C做匀速圆周运动,由几何关系得出AB的距离,由运动学基本公式分析即可求解.
解答 解:A、质点从O到A做匀加速直线运动,水平方向上的位移:a=$\frac{1}{2}$a′t2,
从A到B做类平抛运动,水平方向上的位移:x=vt=a′t2=2a,竖直方向上的位移y═$\frac{1}{2}$a′t2=a,由几何关系可得:O、B两点距离为:s=$\sqrt{(a+2a)^{2}+{a}^{2}}$=$\sqrt{10}$a,故A错误;
B、设到达A点的速度为v,B点的速度为$\sqrt{2}$v,方向与水平方向成45°,B到C点做匀速圆周运动,有:4F=m$\frac{(\sqrt{2}v)^{2}}{r}$,
由匀变速直线运动的速度位移公式可知,在OA段:v2=2$\frac{F}{m}$a,解得:r=a,因此C点与x轴的距离为:(2+$\frac{\sqrt{2}}{2}$)a=$\frac{4+\sqrt{2}}{2}$a,故B错误,C正确.
D、质点从B点运动到C点所用的时间可能为:t′=$\frac{s}{2v}$=$\frac{\frac{3}{4}πr}{\sqrt{2}v}$,OA段有:a=$\frac{v}{2}$t,则质点从O点运动到C点所用时间可能为:t+$\frac{3\sqrt{2}πt}{16}$,故D错误.
本题选错误的,故选:ABD.
点评 本题是一道综合题,物体运动过程复杂,难度较大,分析清楚物体运动过程是解题的前提,解决本题的关键知道质点经历了匀加速直线运动,类平抛运动,匀速圆周运动,结合运动学公式灵活求解.

练习册系列答案
相关题目
2. 某质点做直线运动,运动速率的倒数1/v与位移x的关系如题图所示,关于质点运动的下列说法正确的是( )
某质点做直线运动,运动速率的倒数1/v与位移x的关系如题图所示,关于质点运动的下列说法正确的是( )
 某质点做直线运动,运动速率的倒数1/v与位移x的关系如题图所示,关于质点运动的下列说法正确的是( )
某质点做直线运动,运动速率的倒数1/v与位移x的关系如题图所示,关于质点运动的下列说法正确的是( )| A. | 质点做匀加速直线运动 | |
| B. | $\frac{1}{v}$-x图线斜率等于质点运动加速度 | |
| C. | 四边形AA′B′B面积可表示质点运动时间 | |
| D. | 四边形BB′C′C面积可表示质点运动时间 |
9.下列说法中正确的是( )
| A. | 温度高的物体比温度低的物体热量多 | |
| B. | 热量能从低温物体传向高温物体 | |
| C. | 温度高的物体比温度低的物体分子热运动的平均动能大 | |
| D. | 相互间达到热平衡的两物体的内能一定相等 | |
| E. | 分子势能随着分子间距离的增大,可能先减小后增大 |
19.下列说法中正确的是( )
| A. | 一定质量的理想气体经过绝热压缩,气体的温度升高、压强增大 | |
| B. | 浸润现象是由于附着层的液体分子比液体内部稀疏,分子间作用表现为引力造成的 | |
| C. | 在一定温度下,饱和汽的分子数密度是一定的 | |
| D. | 一切自发过程总是沿着熵增加的方向进行 | |
| E. | 能量耗散使能的总量减少,也导致能量品质的降低 |
6.如图是一沿直线运动的质点在t=0到t=4s内的vt图象.从图中可以看出( )


| A. | 质点的速度方向在0~4s内始终未变 | |
| B. | 质点的加速度方向在0~4s内始终未变 | |
| C. | 在1~2s内质点的加速度数值最小 | |
| D. | 在3~4s内质点运动的距离最大 |
17.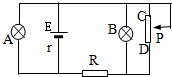 在如图所示的电路中,A、B为相同的两个灯泡,当变阻器的滑动头向C端滑动时( )
在如图所示的电路中,A、B为相同的两个灯泡,当变阻器的滑动头向C端滑动时( )
 在如图所示的电路中,A、B为相同的两个灯泡,当变阻器的滑动头向C端滑动时( )
在如图所示的电路中,A、B为相同的两个灯泡,当变阻器的滑动头向C端滑动时( )| A. | A灯变亮,B灯变暗 | B. | A灯变暗,B灯变亮 | C. | A、B灯均变亮 | D. | A、B灯均变暗 |
 真空中有三个点电荷,它们固定在边长50cm的等边三角形的三个顶点上,每个点电荷都是+2×10-6C,求它们所受的库仑力?
真空中有三个点电荷,它们固定在边长50cm的等边三角形的三个顶点上,每个点电荷都是+2×10-6C,求它们所受的库仑力? 如图所示,A是地球的同步卫星,另一卫星B的圆形轨道位于赤道平面内,且与同步卫星绕行方向相同,已知同步卫星的轨道半径为R,B卫星的轨道半径为4R,某时刻A、B卫星转到同一半径上,求:
如图所示,A是地球的同步卫星,另一卫星B的圆形轨道位于赤道平面内,且与同步卫星绕行方向相同,已知同步卫星的轨道半径为R,B卫星的轨道半径为4R,某时刻A、B卫星转到同一半径上,求: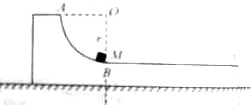 如图所示,光滑水平面N上有一质量为M的滑块,AB段为光滑球面的$\frac{1}{4}$圆弧,半径为r,BC段是粗糙的水平面,长为l.一质量为m的物块,从A点由静止释放,沿ABC滑行,最后停在C点,求:
如图所示,光滑水平面N上有一质量为M的滑块,AB段为光滑球面的$\frac{1}{4}$圆弧,半径为r,BC段是粗糙的水平面,长为l.一质量为m的物块,从A点由静止释放,沿ABC滑行,最后停在C点,求: