题目内容
17. 在做“探究平抛运动”的实验时,实验小组让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹.
在做“探究平抛运动”的实验时,实验小组让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹.(1)为了能较准确地描绘运动轨迹,下面列出了一些操作要求,将你认为正确的选项前面的字母填在横线上C. (只有一项正确.)
A.用铅笔记录小球位置时,每次必须严格地等距离下降
B.为了减小误差,应尽量减小小球和轨道的摩擦
C.该实验需要重垂线
D.将球的位置记录在纸上后,取下纸,用直尺将点连成折线
(2)一次实验中,某同学只记录了A、B、C三个点而忘了标记抛出点的位置.今取A为坐标原点,建立了如图所示的坐标系,x为水平方向,y为竖直方向,平抛轨迹上三点的坐标值图中已标出,则小球平抛初速度v0=1m/s,平抛起点的纵坐标为(-10,-5)cm.(g=10m/s2)
分析 平抛运动分解为:水平方向的匀速直线运动,竖直方向的自由落体运动.从图中坐标可看出,物体从A→B→C的水平位移一样,都为10cm,设为△x,说明各段的时间相等,设为T,可知△x=v0T,由运动的等时性,T由竖直方向运动求出,从A→B→C的竖直位移依次相差△h=10cm,由匀变速直线运动的规律得△h=gT2,联立可求出初速度v0.再有中间时刻的瞬时速度等于这段时间的平均速度规律求出B点的竖直速度VBy,接着用VBy=VAy+gT和VAy=gt求出从抛出到A点的时间t,这样可求出从抛出到A点的水平位移x=v0t和竖直位移y=$\frac{1}{2}$gt2,那么就可以求出小球开始做平抛运动的位置坐标(x,y分别在x轴、y轴的负半轴,应为负值.)
解答 解:(1)A、用铅笔记录小球位置时,每次必须严格控制相等水平距离,并不是等距离下降在,故A错误;
B、小球和轨道的摩擦力,不会影响小球初水平抛出,故B错误;
C、实验需要重垂线,从而确定竖直平面,故C正确;
D、球的位置记录在纸上后,取下纸,用直尺将点平滑连接,故D错误;
故选:C;
(2)从坐标中可看出从A→B→C的水平位移一样,都为△x=10cm,说明各段的时间相等,设为T,可知:
△x=v0T,分析A→B→C的竖直位移依次相差△h=10cm,由匀变速直线运动的规律得:△h=gT2,
联立可求出初速度v0=△x$\sqrt{\frac{g}{△h}}$,代入数值得v0=0.1×$\sqrt{\frac{10}{0.1}}$m/s=1m/s.
由中间时刻的瞬时速度等于这段时间的平均速度得B的竖直速度:VBy=$\frac{{h}_{AC}}{2T}$=$\frac{0.4}{2}$×$\sqrt{\frac{10}{0.1}}$m/s=2m/s,
又VBy=VAy+gT,因此VAy=VBy-gT=2m/s-10×0.1m/s=1m/s,
又VAy=gt,所以从抛出到A点的时间t=$\frac{{v}_{Ay}}{g}$=$\frac{1}{10}$s=0.1s,
因此从抛出到A点的水平位移x=v0t=1.0×0.1 m=0.1m=10cm,
竖直位移y=$\frac{1}{2}$gt2=$\frac{1}{2}$×10×(0.1)2m=0.05m=5cm,
那么物体开始做平抛运动的位置坐标(-10cm,-5cm).
故答案为:(1)C;(2)1,(-10,-5).
点评 平抛运动分解为:水平方向的匀速直线运动,竖直方向的自由落体运动.由坐标分析物体水平方向和竖直方向的运动特点,充分利用匀变速直线运动的规律来求解,所求的坐标为负值.


| A. | 沿纸面向上移动 | B. | 沿纸面向下移动 | C. | 沿NN′直线移动 | D. | 绕OO′轴转动 |
| A. | 2$\sqrt{2}$v | B. | $\sqrt{2}$v | C. | 2v | D. | $\frac{v}{2}$ |

| A. | 质点甲向所选定的正方向运动,质点乙与甲的运动方向相反 | |
| B. | 质点甲、乙的速度不相同 | |
| C. | 在相同的时间内,质点甲、乙的位移相同 | |
| D. | 甲、乙之间的距离不一定越来越大 |
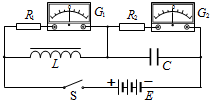 图中L为自感系数足够大的理想电感,C是电容量足够大的理想电容,R1、R2是阻值大小合适的相同电阻,G1、G2是两个零刻度在中央的相同的灵敏电流表,且电流从哪一侧接线柱流入指针即向哪一侧偏转,E是可以不计内阻的直流电源.针对该电路下列判断正确的是( )
图中L为自感系数足够大的理想电感,C是电容量足够大的理想电容,R1、R2是阻值大小合适的相同电阻,G1、G2是两个零刻度在中央的相同的灵敏电流表,且电流从哪一侧接线柱流入指针即向哪一侧偏转,E是可以不计内阻的直流电源.针对该电路下列判断正确的是( )| A. | 电键S闭合的瞬间,仅电流计G1发生明显地偏转 | |
| B. | 电键S闭合的瞬间,两电流计将同时发生明显的偏转 | |
| C. | 电路工作稳定后,两电流计均有明显不为零的恒定示数 | |
| D. | 电路工作稳定后再断开电键S,此后的短时间内,G1的指针将向右偏转,G2的指针将向左偏转 |
 如图所示,电梯质量为M,地板上放置一质量为m的物体.钢索拉电梯由静止开始向上加速运动,当上升高度为H时,速度达到v,则( )
如图所示,电梯质量为M,地板上放置一质量为m的物体.钢索拉电梯由静止开始向上加速运动,当上升高度为H时,速度达到v,则( )| A. | 地板对物体的支持力做的功等于mgH | |
| B. | 电梯重力势能的增量为$\frac{1}{2}$Mv2+MgH | |
| C. | 合力对电梯做的功等于$\frac{1}{2}$Mv2 | |
| D. | 地板对物体的支持力做的功等于$\frac{1}{2}$mv2 |
 如图所示,在一静止小车上有一水平横杆AB,可绕过中点O的水平轴无摩擦转动,A端用细绳挂一重物,B端用一竖直轻弹簧连于车上,当重物在水平向左的恒力F作用下被向左拉起后,与原来相比悬挂重物的细绳张力大小将变大,弹簧的伸长量将不变.(填变大,变小或不变)
如图所示,在一静止小车上有一水平横杆AB,可绕过中点O的水平轴无摩擦转动,A端用细绳挂一重物,B端用一竖直轻弹簧连于车上,当重物在水平向左的恒力F作用下被向左拉起后,与原来相比悬挂重物的细绳张力大小将变大,弹簧的伸长量将不变.(填变大,变小或不变)
