题目内容
1.下列说法中符合实际的是( )| A. | 变化的磁场一定产生变化的电场 | |
| B. | 电磁波不能发生衍射现象 | |
| C. | 根据多普勒效应可以判断遥远天体对地球的运动速度 | |
| D. | 光在真空中的运动速度在不同惯性系中测得数值可能不同 |
分析 均匀变化的磁场产生稳定的电场,非均匀变化的磁场产生变化的电场;电磁波是横波,波都能发生干涉和衍射;利用多普勒效应和光速不变原理判断CD选项即可.
解答 解:A、只有非均匀变化的磁场才一定产生变化的电场,若是均匀变化的磁场,则会产生恒定的电场,故A错误;
B、电磁波是横波,波都能发生干涉和衍射,故B错误;
C、由于波源与接受者的相对位移的改变,而导致接受频率的变化,称为多普勒效应,所以可以判断遥远天体相对于地球的运动速度,故C正确;
D、根据光速不变原理,知在不同惯性系中,光在真空中沿不同方向的传播速度大小相等,故D错误.
故选:C.
点评 明确干涉和衍射是波特有的现象;知道电磁波谱及作用功能,多普勒效应和光速不变原理,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
11. 矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中,输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中,输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
 矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中,输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中,输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )| A. | 1s末线框平面垂直于磁场,穿过线框的磁通量变化最快 | |
| B. | 2s末线框平面垂直于磁场,穿过线框的磁通量最大 | |
| C. | 交流电压的有效值为36$\sqrt{2}$V,频率为0.25Hz | |
| D. | 用该交流电为额定电压36V的机床照明灯供电,照明灯恰好可以正常发光 |
12.关于下列四幅图的说法正确的是( )
| A. | 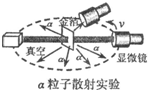 旋转显微镜时能在不同位置观察到数量相同的a粒子 | |
| B. |  用紫外线照射原来不带电的锌板时发现验电器的指针张开一定角度 | |
| C. |  黑体的辐射强度随温度的升高而变强,且峰值向频率变小的方向移动 | |
| D. |  丙为a射线,它的电离作用很强,可消除静电 |
6.影响物质材料电阻率的因素很多,一般金属材料的电阻率随温度的升高而增大,而半导体材料的电阻率则与之相反,随温度的升高而减少.某课题研究组需要研究某种导电材料的导电规律,他们用该种导电材料制作成电阻较小的线状元件Z做实验,测量元件Z中的电流随两端电压从零逐渐增大过程中的变化规律.
(1)他们应选用图1的哪个电路进行实验?A

(2)实验测得元件Z的电压与电流的关系如表所示.
根据表中数据,判断元件Z是半导体材料(选填“金属”、“半导体”);
(3)用螺旋测微器测得线状元件Z的直径如图2所示,则元件Z的直径是1.990mm;
(4)把元件Z接入如图3所示的电路中,当电阻R的阻值为2Ω时电流表的读数为1.25A;当电阻R的阻值为3.6Ω时电流表的读数为0.80A.结合上表数据可求得电池的电动势为E=4V,内阻为r=0.4Ω.
(1)他们应选用图1的哪个电路进行实验?A

(2)实验测得元件Z的电压与电流的关系如表所示.
| U/V | 0 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.50 | 1.60 |
| I/A | 0 | 0.20 | 0.45 | 0.80 | 1.25 | 1.80 | 2.80 | 3.20 |
(3)用螺旋测微器测得线状元件Z的直径如图2所示,则元件Z的直径是1.990mm;
(4)把元件Z接入如图3所示的电路中,当电阻R的阻值为2Ω时电流表的读数为1.25A;当电阻R的阻值为3.6Ω时电流表的读数为0.80A.结合上表数据可求得电池的电动势为E=4V,内阻为r=0.4Ω.
13. 我国未来将在月球地面上建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆轨道的近月点B处与空间站C对接.已知空间站绕月圆轨道的半径为r,周期为T,万有引力常量为G,月球的半径为R.下列说法中错误的是( )
我国未来将在月球地面上建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆轨道的近月点B处与空间站C对接.已知空间站绕月圆轨道的半径为r,周期为T,万有引力常量为G,月球的半径为R.下列说法中错误的是( )
 我国未来将在月球地面上建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆轨道的近月点B处与空间站C对接.已知空间站绕月圆轨道的半径为r,周期为T,万有引力常量为G,月球的半径为R.下列说法中错误的是( )
我国未来将在月球地面上建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆轨道的近月点B处与空间站C对接.已知空间站绕月圆轨道的半径为r,周期为T,万有引力常量为G,月球的半径为R.下列说法中错误的是( )| A. | 航天飞机在图示位置正在加速向B运动 | |
| B. | 月球的第一宇宙速度为v=$\frac{2πr}{T}$ | |
| C. | 月球的质量为M=$\frac{{4{π^2}{r^3}}}{{G{T^2}}}$ | |
| D. | 要使航天飞机和空间站对接成功,飞机在接近B点时必须减速 |
4.星球上的物体脱离该星球引力所需的最小速度称为第二宇宙速度,星球的第二宇宙速度v2与第一宇宙速度v1的关系是v2=$\sqrt{2}$v1,已知地球的半径为R,地球表面的重力加速度为g,若某星球的半径为r=2R,该星球表面的重力加速度为地球表面重力加速度的$\frac{1}{8}$,不计其它星球的影响,则该星球的第二宇宙速度为( )
| A. | $\sqrt{2gR}$ | B. | $\sqrt{gR}$ | C. | $\frac{\sqrt{gR}}{2}$ | D. | $\sqrt{\frac{gR}{2}}$ |
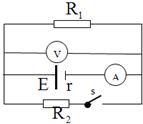 如图所示的电路中,当开关S断开时,电压表V,电流表A的示数分别为2.0V和0.5V,闭合S后它们的示数变为1.0V和1.0A.电压表、电流表均为理想电表.求
如图所示的电路中,当开关S断开时,电压表V,电流表A的示数分别为2.0V和0.5V,闭合S后它们的示数变为1.0V和1.0A.电压表、电流表均为理想电表.求
 某学校研究性学习小组的同学做“验证力的平行四边形定则”实验.
某学校研究性学习小组的同学做“验证力的平行四边形定则”实验.