题目内容
16. 如图所示,物体A和B用轻绳相连,挂在轻弹簧下静止不动,A的质量为m,B的质量为M,弹簧的劲度系数为k.当连接A、B的绳突然断开后,物体A将在竖直方向上做简谐运动,则A振动的振幅为( )
如图所示,物体A和B用轻绳相连,挂在轻弹簧下静止不动,A的质量为m,B的质量为M,弹簧的劲度系数为k.当连接A、B的绳突然断开后,物体A将在竖直方向上做简谐运动,则A振动的振幅为( )| A. | $\frac{(M+m)g}{2k}$ | B. | $\frac{mg}{k}$ | C. | $\frac{(M+m)g}{k}$ | D. | $\frac{Mg}{k}$ |
分析 振幅是振动物体离开平衡位置的最大距离.在平衡位置时,A所受的合外力为零,根据平衡条件和胡克定律求出绳剪断前弹簧伸长的长度和平衡位置弹簧伸长的长度,即可求出振幅.
解答 解:绳剪断前,弹簧伸长的长度 x1=$\frac{(M+m)g}{k}$;
绳剪断后,A做简谐运动,在平衡位置时,弹簧的拉力与重力平衡,此时弹簧伸长的长度为 x2=$\frac{mg}{k}$;
所以A振动的振幅为 A=x1-x2=$\frac{(M+m)g}{k}$-$\frac{mg}{k}$=$\frac{Mg}{k}$.故D正确,ABC错误.
故选:D
点评 正确理解振幅的含义,运用平衡条件和胡克定律求解是解答本题的关键.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
20.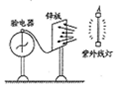 如图所示,1887年德国物理学家赫兹利用紫外线照射锌板后,发现与锌板连接的验电器箔片张开,关于这一现象,下列说法中正确的是( )
如图所示,1887年德国物理学家赫兹利用紫外线照射锌板后,发现与锌板连接的验电器箔片张开,关于这一现象,下列说法中正确的是( )
 如图所示,1887年德国物理学家赫兹利用紫外线照射锌板后,发现与锌板连接的验电器箔片张开,关于这一现象,下列说法中正确的是( )
如图所示,1887年德国物理学家赫兹利用紫外线照射锌板后,发现与锌板连接的验电器箔片张开,关于这一现象,下列说法中正确的是( )| A. | 验电器箔片张开,是因为箔片带负电 | |
| B. | 验电器箔片张开,是因为锌板得到了正电荷 | |
| C. | 紫外线灯功率增大,箔片张角也增大 | |
| D. | 换用红外线灯照射锌板,箔片也一定张开 |
1. 如图所示,带有挡板的光滑斜面固定在水平地面上,斜面倾角θ=30°,质量均为2kg的A、B两物体用轻弹簧拴接在一起,弹簧的劲度系数为5N/cm,质量为4kg的物体C用细线通过光滑的轻质定滑轮与物体B连接,开始时A、B均静止在斜面上,A紧靠在挡板处,用手托住C,使细线刚好被拉直,现把手拿开,让C由静止开始运动,从C开始运动到A刚要离开挡板的过程中,下列说法正确的是(g取10m/s2)( )
如图所示,带有挡板的光滑斜面固定在水平地面上,斜面倾角θ=30°,质量均为2kg的A、B两物体用轻弹簧拴接在一起,弹簧的劲度系数为5N/cm,质量为4kg的物体C用细线通过光滑的轻质定滑轮与物体B连接,开始时A、B均静止在斜面上,A紧靠在挡板处,用手托住C,使细线刚好被拉直,现把手拿开,让C由静止开始运动,从C开始运动到A刚要离开挡板的过程中,下列说法正确的是(g取10m/s2)( )
 如图所示,带有挡板的光滑斜面固定在水平地面上,斜面倾角θ=30°,质量均为2kg的A、B两物体用轻弹簧拴接在一起,弹簧的劲度系数为5N/cm,质量为4kg的物体C用细线通过光滑的轻质定滑轮与物体B连接,开始时A、B均静止在斜面上,A紧靠在挡板处,用手托住C,使细线刚好被拉直,现把手拿开,让C由静止开始运动,从C开始运动到A刚要离开挡板的过程中,下列说法正确的是(g取10m/s2)( )
如图所示,带有挡板的光滑斜面固定在水平地面上,斜面倾角θ=30°,质量均为2kg的A、B两物体用轻弹簧拴接在一起,弹簧的劲度系数为5N/cm,质量为4kg的物体C用细线通过光滑的轻质定滑轮与物体B连接,开始时A、B均静止在斜面上,A紧靠在挡板处,用手托住C,使细线刚好被拉直,现把手拿开,让C由静止开始运动,从C开始运动到A刚要离开挡板的过程中,下列说法正确的是(g取10m/s2)( )| A. | 初状态弹簧的压缩量为2cm | |
| B. | 末状态弹簧的伸长量为2cm | |
| C. | 物体B、C组成的系统机械能守恒 | |
| D. | 物体C克服绳的拉力所做的功为0.8J |
4.如图(1)所示,在粗糙的水平地面上,放有一块质量为m=1kg,初速度为v0的木块,现对木块施加水平恒力F,方向与初速度的方向在同一条直线上,通过实验发现,不同的F,物块在地面运动的时间t不同,且当-2N≤F<2N时,$\frac{1}{t}$与F的关系如图(2)所示(设v0的方向为正、滑动摩擦力等于最大静摩擦力),则( )
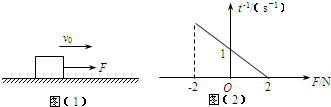

| A. | 物块的初速度为2m/s | B. | 物块与地面间的动摩擦因数为0.2 | ||
| C. | 物块运动的时间可能等于0.4s | D. | 物块运动的时间不可能等于0.4s |
5.一质点做匀加速直线运动,在时间t内的位移为s,该段时间的末速度变为该段时间初速度的5倍.该质点的加速度为( )
| A. | $\frac{2s}{3{t}^{2}}$ | B. | $\frac{16s}{3{t}^{2}}$ | C. | $\frac{8s}{3{t}^{2}}$ | D. | $\frac{4s}{3{t}^{2}}$ |
 一质点做简谐运动,频率为0.5Hz,振幅为4 cm.当振子具有最大正向位移的瞬时开始计时,在图中画出振动图象.(至少一个周期)
一质点做简谐运动,频率为0.5Hz,振幅为4 cm.当振子具有最大正向位移的瞬时开始计时,在图中画出振动图象.(至少一个周期) 2016年8月17日,广西省南宁市上思县至吴圩机场二级路段发生山体滑坡事故,假设在发生山体滑坡时,山坡的底部B处正有一游客逗留,如图所示,此时距坡底160m的山坡A处有一圆形石头正以2m/s的速度、1m/s2的加速度匀加速下滑,游客发现后,立即以0.4m/s2的加速度由静止开始做匀加速直线运动跑离坡底,石头滑到B处前后速度大小不变,但开始以2m/s2的加速度匀减速运动,已知游客从发现圆形石头到开始逃跑的反应时间为1s,游客跑动的最大速度为6m/s,且游客的运动与圆形石头的运动在同一竖直平面内,试求:
2016年8月17日,广西省南宁市上思县至吴圩机场二级路段发生山体滑坡事故,假设在发生山体滑坡时,山坡的底部B处正有一游客逗留,如图所示,此时距坡底160m的山坡A处有一圆形石头正以2m/s的速度、1m/s2的加速度匀加速下滑,游客发现后,立即以0.4m/s2的加速度由静止开始做匀加速直线运动跑离坡底,石头滑到B处前后速度大小不变,但开始以2m/s2的加速度匀减速运动,已知游客从发现圆形石头到开始逃跑的反应时间为1s,游客跑动的最大速度为6m/s,且游客的运动与圆形石头的运动在同一竖直平面内,试求: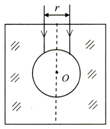 一边长为4r的立方体玻璃介质放置于水平桌面上,其中心有一直径为2r的球形空气泡,直径为r的圆柱形平行单色光束垂立方体上表面入射,光束的中心轴过球形气泡的中心.其截面图如图所示,已知该玻璃介质对此单色光的折射率为$\sqrt{2}$,光在真空中的转播速度为3×108m/s.求:
一边长为4r的立方体玻璃介质放置于水平桌面上,其中心有一直径为2r的球形空气泡,直径为r的圆柱形平行单色光束垂立方体上表面入射,光束的中心轴过球形气泡的中心.其截面图如图所示,已知该玻璃介质对此单色光的折射率为$\sqrt{2}$,光在真空中的转播速度为3×108m/s.求: