题目内容
如图所示，板长为L的平行板电容器倾斜固定放置，极板与水平线夹角θ＝30°，某时刻一质量为m、带电荷量为q的小球由正中央A点静止释放，小球离开电场时速度是水平的(提示：离开的位置不一定是极板边缘)，落到距离A点高度为h的水平面处的B点，B点放置一绝缘弹性平板M，当平板与水平夹角α＝45°时，小球恰好沿原路返回A点．求：
(1)电容器极板间的电场强度E；
(2)平行板电容器的板长L；
(3)小球在A、B间运动的周期T.
(1)电容器极板间的电场强度E；
(2)平行板电容器的板长L；
(3)小球在A、B间运动的周期T.
(1)
(2)3h (3)2
(2)3h (3)2(1)带电粒子沿水平方向做匀加速运动，可知：
qEcos θ＝mg ①
故E＝.
(2)小球垂直落到弹性挡板上，且α＝45°
则有v0＝vy＝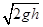
②
由动能定理得：qE·
Ltan θ＝mv
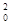③
由②③得：L＝3h.
(3)由小球在电场中做匀加速运动
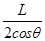＝gtan θ·t
t1＝
＝
平抛运动的时间为t2＝
总时间为：
t＝2t1＋2t2＝2.
qEcos θ＝mg ①
故E＝
.(2)小球垂直落到弹性挡板上，且α＝45°
则有v0＝vy＝
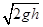②由动能定理得：qE·
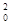Ltan θ＝mv③由②③得：L＝3h.
(3)由小球在电场中做匀加速运动
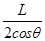＝gtan θ·tt1＝
＝平抛运动的时间为t2＝
总时间为：
t＝2t1＋2t2＝2
.
练习册系列答案
相关题目
，质量之比为
，若两车与路面的动摩擦因数相同，且不计空气阻力，当汽车急刹车后，甲、乙两车滑行的最大距离S1和S2之比是
的值。
的物体,在水平恒定拉力的作用下以一定的初速度在粗糙的水平面上做匀速运动，当运动一段时间后,拉力逐渐减小，且当拉力减小到零时，物体刚好停止运动，图中给出了拉力随位移变化的关系图象。已知重力加速度g =10m/s2，由此可知
s
，
，偏转电场极板长
、板间距
，
）求：
