题目内容
12. 如图所示,在直角坐标系的第Ⅰ、Ⅱ象限分布着方向水平向左的匀强电场,Ⅲ、Ⅳ象限分布着竖直向上的匀强电场,电场强度大小相等.Ⅲ、Ⅳ象限还分布着垂直纸面向里、磁感应强度为B=$\sqrt{2}$T的匀强磁场.现从电场中A(0.4m,0.4m)点由静止释放一质量m=0.1kg,q=0.5C的带正电微粒,该微粒第一次进入磁场时恰过O点,g=10m/s2,求:
如图所示,在直角坐标系的第Ⅰ、Ⅱ象限分布着方向水平向左的匀强电场,Ⅲ、Ⅳ象限分布着竖直向上的匀强电场,电场强度大小相等.Ⅲ、Ⅳ象限还分布着垂直纸面向里、磁感应强度为B=$\sqrt{2}$T的匀强磁场.现从电场中A(0.4m,0.4m)点由静止释放一质量m=0.1kg,q=0.5C的带正电微粒,该微粒第一次进入磁场时恰过O点,g=10m/s2,求:(1)匀强电场的电场强度E的大小;
(2)微粒进入磁场做何运动,第一次离开磁场时的位置B坐标及从A到B点所用时间;
(3)微粒第一、二次射入磁场位置间距离.
分析 (1)根据微粒从A由静止运动到O点,结合微粒受到电场力与重力,即可判定运动情况,再依据F=qE,即可求解电场强度;
(2)根据电场力等于重力,则有微粒进入磁场后,由洛伦兹力提供向心力,做匀速圆周运动,结合进入的速度大小与方向,并由半径公式,从而求得B坐标,再由周期公式,结合圆弧对应的圆心角,即可求解;
(3)根据电场力与重力大小与方向,从而确定微粒的运动情况,进而确定微粒第二次进入磁场的位置,最后求得两者间距.
解答 解:(1)微粒由A点静止运动到O点,因A坐标(0.4m,0.4m),
因此可判定微粒做匀加速直线运动,且重力大小等于电场力,
即mg=qE,
解得:E=$\frac{mg}{q}$=$\frac{0.1×10}{0.5}$=2V/m;
(2)根据带正电微粒,当进入磁场时,则受到竖直向上的电场力,与重力恰好平衡,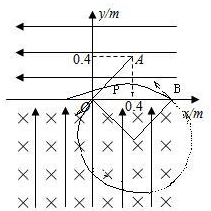
那么受到洛伦兹力提供向心力,做匀速圆周运动,
由运动学公式,微粒进入磁场的速度v=$\sqrt{2ax}$=$\sqrt{2×\sqrt{2}g×0.4\sqrt{2}}$=4m/s;
且速度方向与x轴夹角为45°;
根据半径公式r=$\frac{mv}{qB}$=$\frac{0.1×4}{0.5×\sqrt{2}}$=0.4$\sqrt{2}$m
由于微粒以45°进入磁场,则在磁场中运动轨迹为$\frac{3}{4}$圆,
那么OB间距为d=$\sqrt{2}$r=0.8m
即第一次离开磁场时的位置B坐标(0.8,0)
从O到B点所用时间t2=$\frac{3}{4}T$=$\frac{3}{4}×\frac{2π×0.1}{0.5×\sqrt{2}}$≈0.67s;
而从A到O点的时间为t1=$\frac{v}{a}=\frac{4}{\sqrt{2}×10}$=0.28s
因此从A到B点所用时间t=0.67+0.28=0.95s
(3)当微粒以4m/s的速度与x轴夹角为45°,进入电场后,受到与速度方向垂直,大小为$\sqrt{2}$g加速度做类平抛运动,将运动分解成竖直方向与水平方向,
则有:vy=gt
解得:t=$\frac{4×\frac{\sqrt{2}}{2}}{10}$=0.2$\sqrt{2}$s;
因此在电场力方向,发生位移为x=vxt+$\frac{1}{2}a{t}^{2}$=$2\sqrt{2}×0.2\sqrt{2}+\frac{1}{2}×10×(0.2\sqrt{2})^{2}$=1.2m
那么第一、二次射入磁场位置间距离为△d=1.2-0.8=0.4m
答:(1)匀强电场的电场强度E的大小2V/m;
(2)微粒进入磁场做匀速圆周运动,第一次离开磁场时的位置B坐标(0.8m,0)
及从A到B点所用时间0.95s;
(3)微粒第一、二次射入磁场位置间距离0.4m.
点评 本题重点是画出带电粒子的运动轨迹,当是类平抛运动时,则可分解成沿电场强度方向是匀加速,垂直电场强度方向是匀速.当是圆周运动时,可由几何关系去找到已知长度与半径的关系,最终能求出结果.

 如图所示,A球用线悬挂且通过弹簧与B球相连,两球质量相等,当两球都静止时,将悬线烧断,不计空气阻力,下列说法正确的是( )
如图所示,A球用线悬挂且通过弹簧与B球相连,两球质量相等,当两球都静止时,将悬线烧断,不计空气阻力,下列说法正确的是( )| A. | 线断瞬间,A球的加速度大于B球的加速度 | |
| B. | 线断后最初一段时间里,重力势能转化为动能和弹性势能 | |
| C. | 在下落过程中,两小球、弹簧和地球组成的系统机械能守恒 | |
| D. | 线断后最初一段时间里,动能增加大于重力势能的减小 |
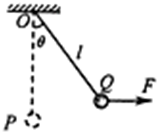 如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,初始时刻小球静止于P点,第一次小球在水平拉力F作用下,从P点缓慢地移动到Q点,此时轻绳与竖直方向夹角为θ,张力大小为T1,第二次在水平恒力F′作用下,从P点开始运动并恰好能到达Q点,至Q点时轻绳中的张力大小为T2,不计空气阻力,重力加速度为g,关于这两个过程,下列说法中正确的是( )
如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,初始时刻小球静止于P点,第一次小球在水平拉力F作用下,从P点缓慢地移动到Q点,此时轻绳与竖直方向夹角为θ,张力大小为T1,第二次在水平恒力F′作用下,从P点开始运动并恰好能到达Q点,至Q点时轻绳中的张力大小为T2,不计空气阻力,重力加速度为g,关于这两个过程,下列说法中正确的是( )| A. | 两个过程中,轻绳的张力均变大 | |
| B. | 第一个过程中,拉力F在逐渐变大,且最大值一定大于F′ | |
| C. | T1=$\frac{mg}{cosθ}$,T2=mg | |
| D. | 第二个过程中,重力和水平恒力F′的合力的功率先增大后减小 |
| A. | 物体做匀速圆周运动 | B. | 物体做匀变速直线运动 | ||
| C. | 物体做自由落体运动 | D. | 物体做平抛运动 |
| A. | 伽利略发现万有引力定律得出万有引力常量 | |
| B. | 开普勒提出行星运动规律,并发现了万有引力定律 | |
| C. | 万有引力常量是卡文迪许通过实验测量并计算得出的 | |
| D. | 牛顿发现了万有引力定律并通过精确的计算得出万有引力常量 |
 如图,PQ是电场中的一条电场线,一带电微粒仅在电场力作用下,从a点沿电场线运动到b点,且速度在不断增大,则下列说法中正确的是( )
如图,PQ是电场中的一条电场线,一带电微粒仅在电场力作用下,从a点沿电场线运动到b点,且速度在不断增大,则下列说法中正确的是( )| A. | 该电场一定是匀强电场 | B. | a点电势一定大于b点电势 | ||
| C. | a点场强一定小于b点场强 | D. | a到b过程中带电微粒电势能减少 |
| A. | +q在A点的电势能比在B点大,则B点的电势高 | |
| B. | -q在C点的电势能比在D点大,则C点的电势高 | |
| C. | +q在E点的电势能为负值,-q在F点的电势能为负值,则F点的电势高 | |
| D. | 以上说法都不正确 |
 如图所示,水平轨道AB与竖直半圆轨道BD相切于B点,半圆轨道的半径为R,整个轨道处于竖直向下的电场强度为E的匀强电场中.一个质量为m,带电量为+q的小球从水平
如图所示,水平轨道AB与竖直半圆轨道BD相切于B点,半圆轨道的半径为R,整个轨道处于竖直向下的电场强度为E的匀强电场中.一个质量为m,带电量为+q的小球从水平 在“研究电磁感应现象”的实验中,首先按图1接线,当闭合开关S时,观察到电流表指针向左偏,不通电时电流表指针停在正中央•然后按图2所示将电流表与线圈B连成一个闭合回路,将线圈A、电池、滑动变阻器R′和电键S串联成另一个闭合电路.
在“研究电磁感应现象”的实验中,首先按图1接线,当闭合开关S时,观察到电流表指针向左偏,不通电时电流表指针停在正中央•然后按图2所示将电流表与线圈B连成一个闭合回路,将线圈A、电池、滑动变阻器R′和电键S串联成另一个闭合电路.