题目内容
4.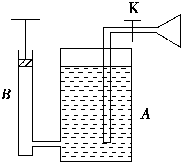 农村常用来喷射农药的压缩喷雾器的结构如图所示.A的容积为7.5L,装入药液后,药液上方空气的压强为105Pa,体积为1.5L,关闭阀门K,用打气筒B每次打进105Pa的空气0.25L.(所有过程气体温度保持不变).则:
农村常用来喷射农药的压缩喷雾器的结构如图所示.A的容积为7.5L,装入药液后,药液上方空气的压强为105Pa,体积为1.5L,关闭阀门K,用打气筒B每次打进105Pa的空气0.25L.(所有过程气体温度保持不变).则:(1)要使药液上方气体的压强为4×105Pa,打气筒活塞应打几次?
(2)当A中有4×105Pa的空气后,打开阀门K可喷射药液,直到不能喷射时,A容器剩余多少体积的药液?
分析 (1)气体发生等温变化,应用玻意耳定律求出打气的次数;
(2)当内外气压相等时,药液不再喷出,应用玻意耳定律求出空气的体积,然后求出剩余的药液.
解答 解:(1)设打n次气,以容器A中与打入的气体为研究对象,
其状态参量为:p1=1×105Pa,V1=(1.5+0.25n)L,p2=4×105Pa,V2=1.5L,
由玻意耳定律得:p1V1=p2V2,
代入数据解得:n=18次;
(2)当内外气压相等时,药液不再喷出,此时:p3=1×105Pa,V3=?,
由玻意耳定律得:p2V2=p3V3,
代入数据解得:V3=6L,
剩余药液的体积:△V=V3-V1=7.5-6=1.5L;
答:(1)要使药液上方气体的压强为4×105Pa,打气筒活塞应打18次;
(2)当A中有4×105Pa的空气后,打开阀门K可喷射药液,直到不能喷射时,A容器剩余多少体积的药液为1.5L.
点评 分析清楚气体状态变化过程、求出气体的状态参量、应用玻意耳定律即可正确解题.

练习册系列答案
相关题目
12.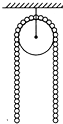 如图所示,一根全长为L 的粗细均匀的铁链,对称地挂在轻小且光滑的定滑轮上.当受到轻微的扰动后,铁链开始滑动,当铁链脱离定滑轮的瞬间,铁链速度的大小为( )
如图所示,一根全长为L 的粗细均匀的铁链,对称地挂在轻小且光滑的定滑轮上.当受到轻微的扰动后,铁链开始滑动,当铁链脱离定滑轮的瞬间,铁链速度的大小为( )
 如图所示,一根全长为L 的粗细均匀的铁链,对称地挂在轻小且光滑的定滑轮上.当受到轻微的扰动后,铁链开始滑动,当铁链脱离定滑轮的瞬间,铁链速度的大小为( )
如图所示,一根全长为L 的粗细均匀的铁链,对称地挂在轻小且光滑的定滑轮上.当受到轻微的扰动后,铁链开始滑动,当铁链脱离定滑轮的瞬间,铁链速度的大小为( )| A. | $\frac{{\sqrt{2gl}}}{2}$ | B. | $\frac{{\sqrt{2gl}}}{3}$ | C. | $\sqrt{2gl}$ | D. | $\sqrt{gl}$ |
19. 下面是“用单摆测定重力加速度”的实验中获得的有关数据:
下面是“用单摆测定重力加速度”的实验中获得的有关数据:
并利用上述数据在图所示的坐标中作出l-T2图象.
①写出l与T2的关系式l=$\frac{g{T}^{2}}{4{π}^{2}}$.
②利用图象,求出重力加速度的值为9.86m/s2.(取π2=9.86 )
 下面是“用单摆测定重力加速度”的实验中获得的有关数据:
下面是“用单摆测定重力加速度”的实验中获得的有关数据:| 摆长l/m | 0.5 | 0.6 | 0.8 | 1.1 |
| 周期T2/s2 | 2.0 | 2.5 | 3.2 | 4.5 |
①写出l与T2的关系式l=$\frac{g{T}^{2}}{4{π}^{2}}$.
②利用图象,求出重力加速度的值为9.86m/s2.(取π2=9.86 )
9.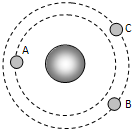 三颗人造地球卫星A、B、C绕地球作匀速圆周运动,如图所示,已知MA=MB<MC,则对于三个卫星,正确的是( )
三颗人造地球卫星A、B、C绕地球作匀速圆周运动,如图所示,已知MA=MB<MC,则对于三个卫星,正确的是( )
 三颗人造地球卫星A、B、C绕地球作匀速圆周运动,如图所示,已知MA=MB<MC,则对于三个卫星,正确的是( )
三颗人造地球卫星A、B、C绕地球作匀速圆周运动,如图所示,已知MA=MB<MC,则对于三个卫星,正确的是( )| A. | 运行线速度关系为vA>vB=vC | |
| B. | 运行周期关系为TA>TB=TC | |
| C. | 向心力大小关系为 FA=FB=FC | |
| D. | 半径与周期关系为$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
16.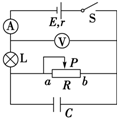 在如图所示的电路中,电源电动势为E,电源内阻为r,闭合开关S,待电流达到稳定后将滑动变阻器的滑动触头P从图示位置向a端移动一些,则待电流再次达到稳定后,与P移动前相比( )
在如图所示的电路中,电源电动势为E,电源内阻为r,闭合开关S,待电流达到稳定后将滑动变阻器的滑动触头P从图示位置向a端移动一些,则待电流再次达到稳定后,与P移动前相比( )
 在如图所示的电路中,电源电动势为E,电源内阻为r,闭合开关S,待电流达到稳定后将滑动变阻器的滑动触头P从图示位置向a端移动一些,则待电流再次达到稳定后,与P移动前相比( )
在如图所示的电路中,电源电动势为E,电源内阻为r,闭合开关S,待电流达到稳定后将滑动变阻器的滑动触头P从图示位置向a端移动一些,则待电流再次达到稳定后,与P移动前相比( )| A. | 电流表示数变小,电压表示数变大 | B. | 小灯泡L变亮 | ||
| C. | 电容器C的电荷量减小 | D. | 电源的总功率变小 |
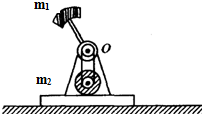 如图是电动打夯机的结构示意图,电动机带动质量为m1的重锤(重锤可视为质点)绕转轴O匀速转动,重锤转动半径为R.电动机连同打夯机底座的质量为m2,重锤和转轴O之间连接杆的质量可以忽略不计,重力加速度为g.
如图是电动打夯机的结构示意图,电动机带动质量为m1的重锤(重锤可视为质点)绕转轴O匀速转动,重锤转动半径为R.电动机连同打夯机底座的质量为m2,重锤和转轴O之间连接杆的质量可以忽略不计,重力加速度为g.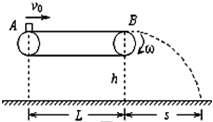 如图甲所示,水平传送带AB的长度L=3.75m,皮带轮的半径R=0.1m.现有一小物体(视为质点)以水平速度v0从A点滑上传送带,物块与传送带间动摩擦因数为μ=0.2,传送带上表面距地面的高度h=5m,g取10m/s2,试讨论下列问题:
如图甲所示,水平传送带AB的长度L=3.75m,皮带轮的半径R=0.1m.现有一小物体(视为质点)以水平速度v0从A点滑上传送带,物块与传送带间动摩擦因数为μ=0.2,传送带上表面距地面的高度h=5m,g取10m/s2,试讨论下列问题: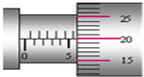
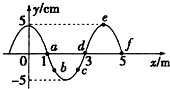 如图所示是一列简谐横波在某时刻的波动图象,从该时刻开始,此波中d质点第一次到达波谷的时间比e质点第一次到达波谷的时间早0.10s.若b质点的平衡位置为x=$\frac{4}{3}$m时,求
如图所示是一列简谐横波在某时刻的波动图象,从该时刻开始,此波中d质点第一次到达波谷的时间比e质点第一次到达波谷的时间早0.10s.若b质点的平衡位置为x=$\frac{4}{3}$m时,求