题目内容
20.在倾角为θ的足够长的斜面顶端有一个小球以初速度v0作平抛运动,重力加速度为g,则根据以上条件可求出的物理量是( )| A. | 小球落到斜面上时的动能 | |
| B. | 小球从抛出到落到斜面上时的运动时间 | |
| C. | 小球在斜面上的落点到抛出点间的距离 | |
| D. | 小球落到斜面上时的速度方向与斜面间的夹角 |
分析 由题意可知小球位移的方向与水平方向的夹角等于斜面的倾角,则由位移关系可求向小球落在斜面上的时间;再由平抛运动的竖直方向的规律可知各量能否求出.
解答 解:A、B、D、已知位移的与水平方向之间的夹角为θ,而由平抛运动的规律可知,tanθ=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{2{v}_{0}}$,可求得时间为t=$\frac{2{v}_{0}tanθ}{g}$,由vy=gt,可求得竖直分速度,由速度的合成与分解可求得最后末速度的大小和方向,但不知小球的质量,故无法求出小球的动能.故A错误,B正确,D正确;
C、由$y=\frac{1}{2}g{t}^{2}$即可求得竖直位移,再由几何关系可求得MN间的距离,故C正确;
故选:BCD
点评 平抛运动可以分解为水平竖直两个方向的运动,也可以分解为沿斜面和垂直于斜面两个运动,应根据题意灵活选择.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.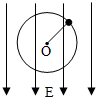 如图所示,竖直向下的匀强电场里,用绝缘细线拴住的带电小球在竖直平面内绕O做匀速圆周运动,则( )
如图所示,竖直向下的匀强电场里,用绝缘细线拴住的带电小球在竖直平面内绕O做匀速圆周运动,则( )
 如图所示,竖直向下的匀强电场里,用绝缘细线拴住的带电小球在竖直平面内绕O做匀速圆周运动,则( )
如图所示,竖直向下的匀强电场里,用绝缘细线拴住的带电小球在竖直平面内绕O做匀速圆周运动,则( )| A. | 带电小球必须带正电 | |
| B. | 带电小球必须带负电 | |
| C. | 带电小球的重力一定小于小球所受的电场力 | |
| D. | 带电小球的重力一定等于小球所受的电场力 |
15. 如图所示,一轻弹簧左端周定在竖直墙壁上,右端与一小滑块相连接,小滑块放在粗糙水平面上,轻弹簧水平.当小滑块在O点时,弹簧处于原长,现用力向左推小滑块压缩弹簧,使小滑块从A点静止释放,小滑块向右运动的最远点为B点(图中B点未画出)小滑块从A向B运动的过程中 ( )
如图所示,一轻弹簧左端周定在竖直墙壁上,右端与一小滑块相连接,小滑块放在粗糙水平面上,轻弹簧水平.当小滑块在O点时,弹簧处于原长,现用力向左推小滑块压缩弹簧,使小滑块从A点静止释放,小滑块向右运动的最远点为B点(图中B点未画出)小滑块从A向B运动的过程中 ( )
 如图所示,一轻弹簧左端周定在竖直墙壁上,右端与一小滑块相连接,小滑块放在粗糙水平面上,轻弹簧水平.当小滑块在O点时,弹簧处于原长,现用力向左推小滑块压缩弹簧,使小滑块从A点静止释放,小滑块向右运动的最远点为B点(图中B点未画出)小滑块从A向B运动的过程中 ( )
如图所示,一轻弹簧左端周定在竖直墙壁上,右端与一小滑块相连接,小滑块放在粗糙水平面上,轻弹簧水平.当小滑块在O点时,弹簧处于原长,现用力向左推小滑块压缩弹簧,使小滑块从A点静止释放,小滑块向右运动的最远点为B点(图中B点未画出)小滑块从A向B运动的过程中 ( )| A. | 加速度先减小后增大.在0点加速度为零 | |
| B. | 速度先增大后减小,在0点速度最大 | |
| C. | 速度先增大后减小,速度最大点在0点左侧 | |
| D. | 0点不是A、B两点间的中点 |
12.以下说法不正确的是( )
| A. | “一江春水向东流”的参照系是江岸 | |
| B. | 我们说“太阳从东方升起”是以太阳为参照系 | |
| C. | 研究表演精彩芭蕾舞的演员的动作时演员可看作质点 | |
| D. | 田径比赛中某运动员跑200米用时25秒,则其平均速度为8m/s |
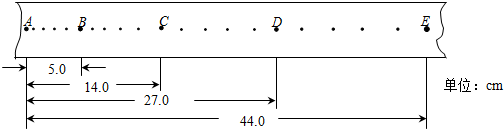
 如图所示,水平桌面由粗糙程度不同的AB、BC两部分组成,且两部分长度相等,小物块p(可视为质点)以初速度v0从A点滑上桌面,最后恰好停在C点,已知物块经过AB与BC两部分所用的时间之比为1:3,且小物块P在AB、BC两段上的运动均可看作匀变速直线运动,求:
如图所示,水平桌面由粗糙程度不同的AB、BC两部分组成,且两部分长度相等,小物块p(可视为质点)以初速度v0从A点滑上桌面,最后恰好停在C点,已知物块经过AB与BC两部分所用的时间之比为1:3,且小物块P在AB、BC两段上的运动均可看作匀变速直线运动,求: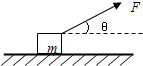 一个质量为m的物体,静止于水平面上,物体与水平面间的动摩擦因数为μ,现用与水平方向成θ角的力F斜向上拉物体,如图,已知重力加速度为g,则
一个质量为m的物体,静止于水平面上,物体与水平面间的动摩擦因数为μ,现用与水平方向成θ角的力F斜向上拉物体,如图,已知重力加速度为g,则 如图所示,木工常用木楔来固定木榫,直角三角形楔子底边长l=35mm,高h=12mm,今用水平力F打入楔子时,木楔自身重力不计,摩擦不计,求:
如图所示,木工常用木楔来固定木榫,直角三角形楔子底边长l=35mm,高h=12mm,今用水平力F打入楔子时,木楔自身重力不计,摩擦不计,求: