题目内容
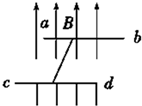如图所示，在同一水平面的两导轨相互平行，并处在竖直向上的匀强磁场中，一根质量为3.6kg，有效长度为2m的金属棒放在导轨上，当金属棒中的电流为5A时，金属棒做匀速直线运动；当金属棒中的电流强度增加到8A时，金属棒能获得2m/s2的加速度．则磁场的磁感应强度为分析：先根据金属棒匀速直线运动时受力平衡，求出所受摩擦力的大小，然后结合牛顿第二定律对加速运动时列方程；利用匀速运动时摩擦力等于安培力求出摩擦因数．
解答：解：金属棒匀速运动时，安培力与摩擦力，则有：f=BI1L
棒加速运动时，由牛顿第二定律可得：BI2L-f=ma
联立得：BI2L-BI1L=ma
代入数据得：B=1.2T
匀速运动时，有：f=BI1L=1.2×5×2N=12N
根据摩擦力公式得：f=μN=μmg
联立以上方程，代入数据得：μ=
=
=
故答案为：1.2；
棒加速运动时，由牛顿第二定律可得：BI2L-f=ma
联立得：BI2L-BI1L=ma
代入数据得：B=1.2T
匀速运动时，有：f=BI1L=1.2×5×2N=12N
根据摩擦力公式得：f=μN=μmg
联立以上方程，代入数据得：μ=
| f |
| mg |
| 12 |
| 3.6×10 |
| 1 |
| 3 |
故答案为：1.2；
| 1 |
| 3 |
点评：本题完全采用力学的方法处理，只要将抓住安培力具有一般力的性质，根据平衡条件和牛顿第二定律进行求解．
练习册系列答案
相关题目
如图所示，在同一水平面上的两金属导轨间距L=O．2m，处在竖直向下的匀强磁场中，磁感应强度B=1T．导体棒ab垂直导轨放置，棒长等于导轨间距，其电阻R=6Ω．闭合开关，当通过导体棒ab的电流I=O.5A时，求：（1）导体棒ab上电流的热功率；（2）导体棒ab受到安培力的大小和方向．
如图所示，在同一水平面上的两金属导轨间距：ab=0.4m，处在竖直向下的匀强磁场中，磁感应强度B=2T．导体棒ab垂直导轨放置在金属导轨间，闭合开关，当通过导体ab的电流I=0.5A，求：
如图所示，在同一水平面上的两根导轨相互平行，并处在竖直向上的匀强磁场中，磁感强度大小为1.2T．一根质量为3.6kg，有效长度为2m的金属棒放在导轨上．当金属棒中的电流为5A时，金属棒做匀速直线运动；当金属棒中的电流增加到8A时，求金属棒的加速度的大小和方向．
如图所示，在同一水平面上的两金属导轨间距：ab=0.2m，处在竖直向下的匀强磁场中，磁感应强度B=1T．导体棒ab垂直导轨放置，棒长等于导轨间距，其电阻R=6Ω．闭合开关，当通过导体ab的电流I=0.5A，求：导体棒ab上电流的热功率为（ ）