题目内容
 如图所示,三根长度均为l的轻绳分别连接于C、D两点,A、B两端被悬挂在水平天花板上,相距2l.现在C点上悬挂一质量为m的重物,为使CD绳保持水平,在D点上可施加一个拉力,则( )
如图所示,三根长度均为l的轻绳分别连接于C、D两点,A、B两端被悬挂在水平天花板上,相距2l.现在C点上悬挂一质量为m的重物,为使CD绳保持水平,在D点上可施加一个拉力,则( )分析:由几何关系可知CD段水平时各绳间的夹角;对结点C分析,由共点力的平衡可求得CD绳水平时绳的拉力;再对结点D分析,由共点力平衡和力的合成可得出最小值.
解答:解:A、B、C、由图可知,要想CD水平,则AC与水平方向的夹角为60°;
结点C受力平衡,则受力分析如图所示:

结点C受到沿AC拉力在水平方向上的分力等于水平向右的拉力T,即:
T=FACcos60°=
FAC
结点C受到沿AC拉力在竖直方向上的分力等于物体的重力,即:
mg=FACsin60°=
FAC
解得:T=
mg;
结点D受力平衡,当拉力F的方向与BD垂直时,力臂最长、最省力,如图所示
最小拉力F=F′=T′cos30°=Tcos30°=
mg×
=
mg
故AC错误,B正确;
D、若该拉力沿AC方向,根据共点力平衡条件,有:
FAC?sin30°+FBD?sin30°=T
FAC?cos30°=FBD?cos30°
解得:FAC=T=
mg,故D正确;
故选:BD.
结点C受力平衡,则受力分析如图所示:

结点C受到沿AC拉力在水平方向上的分力等于水平向右的拉力T,即:
T=FACcos60°=
| 1 |
| 2 |
结点C受到沿AC拉力在竖直方向上的分力等于物体的重力,即:
mg=FACsin60°=
| ||
| 2 |
解得:T=
| ||
| 3 |
结点D受力平衡,当拉力F的方向与BD垂直时,力臂最长、最省力,如图所示
最小拉力F=F′=T′cos30°=Tcos30°=
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
故AC错误,B正确;
D、若该拉力沿AC方向,根据共点力平衡条件,有:
FAC?sin30°+FBD?sin30°=T
FAC?cos30°=FBD?cos30°
解得:FAC=T=
| ||
| 3 |
故选:BD.
点评:在共点力的平衡中要注意几何关系的应用,特别是求最小力时一定要通过几何图形进行分析.

练习册系列答案
相关题目
 (2011?济南一模)如图所示,三根长度均为L的轻绳分别连接于C、D两点,A、B两端被悬挂在水平天花板上,相距2L,现在C点上悬挂一个质量为M的重物,为使CD绳保持水平,在D点上可施加力的最小值为( )
(2011?济南一模)如图所示,三根长度均为L的轻绳分别连接于C、D两点,A、B两端被悬挂在水平天花板上,相距2L,现在C点上悬挂一个质量为M的重物,为使CD绳保持水平,在D点上可施加力的最小值为( )
 C.
C.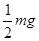 D.
D.


 D.
D.

 C.
C. D.
D.