Question

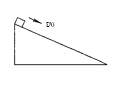
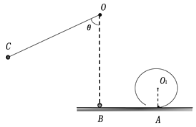
【题目】如图所示，在光滑水平面上A点固定一个底端有小孔的竖直光滑圆弧轨道，圆轨道与水平面在A点相切。小球甲用长为L的轻绳悬挂于O点，O点位于水平面上B点正上方L处。现将小球甲拉至C位置，绳与竖直方向夹角θ=60°，由静止释放，运动到最低点B时与另一静止的小球乙（可视为质点）发生完全弹性碰撞，碰后小球乙无碰撞地经过小孔进入圆弧轨道，当小球乙进入圆轨道后立即关闭小孔。已知小球乙的质量是甲质量的3倍，重力加速度为g。

（1）求甲、乙碰后瞬间小球乙的速度大小；

（2）若小球乙恰好能在圆轨道做完整的圆周运动，求圆轨道的半径。

Answer 1

【答案】（1）；2）。

【解析】

（1）甲球下摆过程，由机械能守恒有：

①

解得②

设甲乙碰撞后速度分别为和，根据动量守恒定律有：

③

根据能量守恒定律有：

④

解得⑤

（2）乙球恰能做圆周运动，则在最高点，根据牛顿第二定律有：

⑥

从最低到最高点，根据动能定理有：

⑦

由⑥⑦得