题目内容
20. 如图所示的电路中,电源电动势E=6V,内阻r=1Ω,R1=R3=2Ω,R2=3Ω,R4=4Ω,若电表是电压表时,其示数为3.07V,若电表是电流表时,其示数为1.5A.
如图所示的电路中,电源电动势E=6V,内阻r=1Ω,R1=R3=2Ω,R2=3Ω,R4=4Ω,若电表是电压表时,其示数为3.07V,若电表是电流表时,其示数为1.5A.
分析 若电表是电压表时电路结构为:R3与R4串联后与R2并联,再与R1串联,接入电源,电压表测量R1和R3的电压之和,若电表是电流表时,电路结构为:R1与R3并联后与R2串联,再与R4并联,接入电源,电流表测量通过R4和R3的电流之和,根据闭合电路欧姆定律结合串并联电路的特点求解即可.
解答 解:若电表是电压表时,电路结构为:R3与R4串联后与R2并联,再与R1串联,接入电源,并联部分电阻${R}_{并}=\frac{({R}_{3}+{R}_{4}){R}_{2}}{{R}_{3}+{R}_{4}+{R}_{2}}=\frac{6×3}{6+3}=2Ω$,
根据闭合电路欧姆定律可知,总电流I=$\frac{E}{{R}_{并}+{R}_{1}+r}=\frac{6}{2+2+1}=1.2A$,
则R1两端的电压U1=R1I=2×1.2=2.4V,并联部分的电压U并=R并I=2×1.2=2.4V,则R3两端的电压${U}_{3}=\frac{{R}_{3}}{{R}_{3}+{R}_{4}}{U}_{并}=\frac{2}{2+4}×2=0.67V$,
所以电压表的示数U=U1+U3=2.4+0.67=3.07V
若电表是电流表时,电路结构为:R1与R3并联后与R2串联,再与R4并联,接入电源,R1与R3并联电阻${R}_{13}={R}_{并}=\frac{{R}_{3}{R}_{1}}{{R}_{3}+{R}_{1}}=\frac{2×2}{2+2}=1Ω$,
则外电路总电阻${R}_{外}=\frac{({R}_{13}+{R}_{2}){R}_{4}}{{R}_{13}+{R}_{4}+{R}_{2}}=\frac{4×4}{4+4}=2Ω$
则总电流I=$\frac{E}{{R}_{外}+r}=\frac{6}{2+1}=2A$,
通过R4的电流${I}_{4}=\frac{{U}_{4}}{{R}_{4}}=\frac{{R}_{外}I}{{R}_{4}}=\frac{2×2}{4}=1A$,
通过R3的电流${I}_{3}=\frac{{U}_{3}}{{R}_{3}}=\frac{\frac{{R}_{13}}{{R}_{13}+{R}_{2}}{U}_{4}}{{R}_{3}}=\frac{\frac{1}{1+3}×4}{2}=0.5A$
则通过电流表的示数I=I3+I4=1+0.5=1.5A.
故答案为:3.07V;1.5A
点评 本题主要考查了闭合电路欧姆定律和电阻的串并联知识,解答本题的关键是能分析清楚电路的结构,知道电压表接在电路中相当于断路,电流表接在电路中相当于导线,难度适中.

 名校课堂系列答案
名校课堂系列答案| A. | 汤姆孙发现电子,提出原子的核式结构模型 | |
| B. | 金属的逸出功随入射光的频率增大而增大 | |
| C. | 核力存在于原子核内所有核子之间 | |
| D. | 核电站是利用重核裂变反应所释放的核能转化为电能 |
| A. | 使人感到舒适的温度约是23℃ | |
| B. | 台灯正常工作时的电流约是2A | |
| C. | 中学生步行的速度约是5m/s | |
| D. | 中学生从一楼匀速上到三楼所做的功约是300J |
 在测量某弹簧的劲度系数时,某同学讲该弹簧沿竖直方向悬挂起来,在另一端挂上不同质量的钩码,测出钩码质量和弹簧长度L的相应数据如表所示:
在测量某弹簧的劲度系数时,某同学讲该弹簧沿竖直方向悬挂起来,在另一端挂上不同质量的钩码,测出钩码质量和弹簧长度L的相应数据如表所示:| 钩码质量(g) | 0 | 20 | 40 | 60 | 80 | 100 |
| 弹簧长度(cm) | 15.0 | 17.1 | 19.0 | 20.9 | 23.0 | 25.1 |
(2)根据所作的图线可得弹簧的劲度系数为10N/m(g取10m/s2).
 高频焊接技术的原理如图(a).线圈接入图(b)所示的正弦式交流电(以电流顺时针方向为正),圈内待焊工件形成闭合回路.则( )
高频焊接技术的原理如图(a).线圈接入图(b)所示的正弦式交流电(以电流顺时针方向为正),圈内待焊工件形成闭合回路.则( )| A. | 图(b)中电流有效值为I | |
| B. | t1~t2时间内工件中的感应电流变大 | |
| C. | 0~t1时间内工件中的感应电流方向为顺时针 | |
| D. | 图(b)中T越大,工件温度上升越快 |
| A. | α粒子散射实验揭示了原子核内部的复杂性 | |
| B. | 光电效应实验揭示了光的粒子性 | |
| C. | 核反应方程中,质量和电荷是守恒的 | |
| D. | 根据玻尔理论可知,一群氢原子核外电子从n=4能级向低能级跃迁最多可辐射6种频率的光子 |
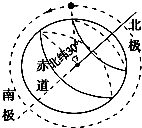 极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,引力常量为G,由以上条件可知( )
极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,引力常量为G,由以上条件可知( )| A. | 地球的质量为$\frac{gR}{G}$ | |
| B. | 卫星运行的线速度为$\frac{πR}{2t}$ | |
| C. | 卫星运行的角速度为$\frac{π}{2t}$ | |
| D. | 卫星距地面的高度为($\frac{4g{R}^{2}{t}^{2}}{{π}^{2}}$)${\;}^{\frac{1}{3}}$ |
 如图所示,有一条长为L.质量为m的均匀金属链条,一半长度在光滑斜面上,斜面倾角为θ,另一半长度沿竖直方向下垂在空中,当从静止开始释放后链条滑动,以斜面最高点所在平面为重力势能的参考平面,求:
如图所示,有一条长为L.质量为m的均匀金属链条,一半长度在光滑斜面上,斜面倾角为θ,另一半长度沿竖直方向下垂在空中,当从静止开始释放后链条滑动,以斜面最高点所在平面为重力势能的参考平面,求: