题目内容
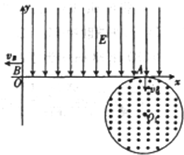 如图所示,x轴上方有竖直向下的匀强电场,从x轴A点(5
如图所示,x轴上方有竖直向下的匀强电场,从x轴A点(5| 3 |
| ||
| 2 |
(1)求匀强电场的电场强度E和圆形磁场的磁感应强度B的大小.
(2)求带电粒子从A点运动到B点的时间.
(3)若粒子在A点可以沿任意方向垂直磁场进入,并使速度大小增为2v0,则粒子在磁场里运动的最长时间.为多少?
分析:采用逆向思维:粒子在电场中只受电场力,做类平抛运动.将速度分解,可求出粒子进入圆形磁场区域时的速度大小.根据牛顿定律求出场强E的大小.粒子在磁场中,洛伦兹力提供向心力,做匀速圆周运动.分析粒子进入磁场的速度方向与进入磁场时的速度方向相同条件,根据圆的对称性,由几何知识得到半径,周期T的表达式.大而确定磁场的磁感应强度B的大小;并由运动学公式可求出从A点运动到B点的时间; 若粒子速度增大时,根据圆心角与周期来确定运动的时间长短.
解答:解:(1)沿着粒子运动反方向研究:粒子从B点射入电场,在电场中作类平抛运动,射出电场时,如图所示.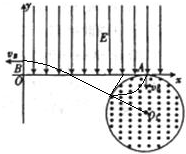
设射出粒子的速度与x轴的夹角为θ,由速度关系,则有:
=cosθ
而vB=
vO,所以解得:θ=30°
则vy=v0sin30°=
在电场力的方向,根据
=2ah与a=
,可得:E=
在x轴方向,粒子的位移,x=vBt=
vB=2
h
粒子射出电场后做匀速运动后,沿着圆形磁场的半径方向射入,经过偏转后从A点射出.
粒子在磁场中由洛伦兹力提供向心力做匀速圆周运动,则有Bqv=m
;
设圆周运动的半径为R,根据几何关系,可得:(5
h-2
h-R)sin30°=R
解得:R=
h
所以,B=
=
(2)粒子做类平抛的运动的时间,t1=
=
=
;
粒子做匀速直线运动的时间为t2,匀速运动的位移为x=
=3h,所以时间t2=
;
粒子做匀速圆周运动的时间为t3,根据入射角度,可知运动轨迹对应的圆心角为120°,则有t3=
×
=
;
则带电粒子从A点运动到B点的时间为t=t1+t2+t3=
h;
(3)速度大小增为2v0,则粒子在磁场中运动半径增加2倍,即为8h,而运动的周期没有变化;当对应的圆心角越大时,运动时间越长.
根据前面可知,圆形磁场的半径与粒子运动的轨道相等,即为4h,当粒子在磁场中运动对应的弦最长,则时间也最长.
最长弦为8h,而粒子运动的半径也为8h,根据几何关系可得,圆心角为60°,所以t=
=
×
=
答:(1)求匀强电场的电场强度
和圆形磁场的磁感应强度B的大小
.
(2)求带电粒子从A点运动到B点的时间
h.
(3)若粒子在A点可以沿任意方向垂直磁场进入,并使速度大小增为2v0,则粒子在磁场里运动的最长时间为
.

设射出粒子的速度与x轴的夹角为θ,由速度关系,则有:
| vB |
| v0 |
而vB=
| ||
| 2 |
则vy=v0sin30°=
| v0 |
| 2 |
在电场力的方向,根据
| v | 2 y |
| qE |
| m |
m
| ||
| 8qh |
在x轴方向,粒子的位移,x=vBt=
| vy |
| a |
| 3 |
粒子射出电场后做匀速运动后,沿着圆形磁场的半径方向射入,经过偏转后从A点射出.
粒子在磁场中由洛伦兹力提供向心力做匀速圆周运动,则有Bqv=m
| v2 |
| R |
设圆周运动的半径为R,根据几何关系,可得:(5
| 3 |
| 3 |
解得:R=
| 3 |
所以,B=
| mv0 |
| qR |
| ||
| 3qh |
(2)粒子做类平抛的运动的时间,t1=
| vy |
| a |
| ||||
|
| 4h |
| v0 |
粒子做匀速直线运动的时间为t2,匀速运动的位移为x=
| R |
| tan30° |
| 3h |
| v0 |
粒子做匀速圆周运动的时间为t3,根据入射角度,可知运动轨迹对应的圆心角为120°,则有t3=
| 1 |
| 3 |
| 2πm |
| qB |
2
| ||
| 3v0 |
则带电粒子从A点运动到B点的时间为t=t1+t2+t3=
21+2
| ||
| 3v0 |
(3)速度大小增为2v0,则粒子在磁场中运动半径增加2倍,即为8h,而运动的周期没有变化;当对应的圆心角越大时,运动时间越长.
根据前面可知,圆形磁场的半径与粒子运动的轨道相等,即为4h,当粒子在磁场中运动对应的弦最长,则时间也最长.
最长弦为8h,而粒子运动的半径也为8h,根据几何关系可得,圆心角为60°,所以t=
| T |
| 6 |
| 1 |
| 6 |
| 2πm |
| Bq |
| ||
| 3v0 |
答:(1)求匀强电场的电场强度
m
| ||
| 8qh |
| ||
| 3qh |
(2)求带电粒子从A点运动到B点的时间
21+2
| ||
| 3v0 |
(3)若粒子在A点可以沿任意方向垂直磁场进入,并使速度大小增为2v0,则粒子在磁场里运动的最长时间为
| ||
| 3v0 |
点评:本题带电粒子在组合场中运动,分别采用不同的方法:电场中运用运动的合成和分解,磁场中圆周运动处理的基本方法是画轨迹.采用逆向思维从而降低解题难度,这通常也是处理题目的一种方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
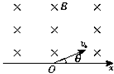 如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹30°角.求正、负离子在磁场中运动半径比
如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹30°角.求正、负离子在磁场中运动半径比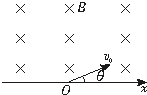 如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中( )?
如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中( )? 如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中( )
如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中( )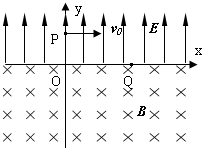 如图所示,x轴上方有一匀强电场,方向与y轴平行;x轴下方有一匀强磁场,方向垂直纸面向里.一质量为m、电量为-q(q>0)的粒子以速度v0从y轴上的P点平行x轴方向射入电场后,从x轴上的Q点进入磁场,并从坐标原点O离开磁场.已知OP=L,OQ=2L.不计重力和一切摩擦,求:
如图所示,x轴上方有一匀强电场,方向与y轴平行;x轴下方有一匀强磁场,方向垂直纸面向里.一质量为m、电量为-q(q>0)的粒子以速度v0从y轴上的P点平行x轴方向射入电场后,从x轴上的Q点进入磁场,并从坐标原点O离开磁场.已知OP=L,OQ=2L.不计重力和一切摩擦,求: