Question

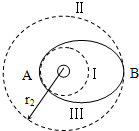
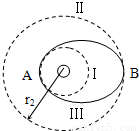
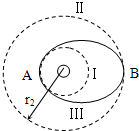随着我国“神舟五号”宇宙飞船的发射和回收成功．标志着我国的航天技术已达到世界先进水平．如图所示，质量为m的飞船绕地球在圆轨道Ⅰ上运行时，半径为r₁，要进入半径为r₂的更高的圆轨道Ⅱ，必须先加速进入一个椭圆轨道Ⅲ，然后再进入圆轨道Ⅱ．已知飞船在圆轨道Ⅱ上运动速度大小为υ，在A点通过发动机向后以速度大小为u（对地）喷出一定质量气体，使飞船速度增加到v′进入椭圆轨道Ⅲ．（已知量为：m、r₁、r₂、υ、v′u）求：
（1）飞船在轨道I上的速度和加速度大小．
（2）发动机喷出气体的质量△m．

Answer 1

分析：（1）飞船在轨道I和Ⅱ上的向心力由万有引力提供，对两个轨道分别根据牛顿第二定律列式，运用比例法求速度和加速度．
（2）根据动量守恒定律mυ₁=（m-△m）υ′-△mu求出探测器在A点喷出的气体质量△m．

解答：解：（1）在轨道I上，有G

Mm

r12

=m

v12

r1

 解得：v1=

GM r1

同理在轨道Ⅱ上 v =

GM r2

 由此得：v1=v

r2 r1

在轨道I上向心加速度为a₁，则有：G

Mm

r12

=ma1
同理在轨道II上向心加速度a=

v2

r2

，则有：G

Mm

r22

=m

v2

r2

由此得：a1=

r2

r12

v2
（2）设喷出气体的质量为△m，由动量守恒得mv₁=（m-△m）v′-△mu      
得：△m=

v′-v r2 r1

v′+u

m
答：
（1）飞船在轨道I上的速度为v

r2 r1

，加速度是

r2

r 2 1

v2．
（2）发动机喷出气体的质量△m为

v′-v r2 r1

v′+u

m．

点评：解决本题的关键掌握万有引力提供向心力G

Mm

r2

=m

v2

r

=ma，以及掌握动量守恒定律．