Question

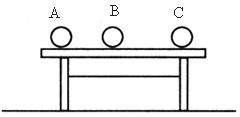
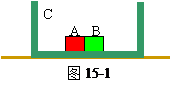在光滑的水平桌面上有一长L=2米的木板C，它的两端各有一块档板，C的质量m_C=5千克，在C的正中央并排放着两个可视为质点的滑块A和B，质量分别为m_A=1千克，m_B=4千克。开始时，A、B、C都处于静止，并且A、B间夹有少量塑胶炸药，如图15-1所示。炸药爆炸使滑块A以6米/秒的速度水平向左滑动，如果A、B与C间的摩擦可忽略，两滑块中任一块与档板碰撞后都与挡板结合成一体，爆炸和碰撞所需时间都可忽略。

(1)当两滑块都与档板相碰撞后，板C的速度多大?

(2)到两个滑块都与档板碰撞为止，板的位移大小和方向如何?

Answer 1

C的位移为：S_C=V_Ct₂=1×0.3=0.3米，方向向左。

解析:

(2)以炸药爆炸到A与C相碰撞经历的时间：t₁=(L/2)/V_A=1/6秒，

在这段时间里B的位移为：S_B=V_Bt₁=1.5×1/6=0.25米，

设A与C相撞后C的速度为V_C，A和C组成的系统水平方向动量守恒：m_AV_A=(m_A+m_C)V_C，

所以V_C=m_AV_A/(m_A+m_C)=1×6/(1+5)=1米/秒

B相对于C的速度为：　 V_BC=V_B-V_C=(-1.5)-(+1)=-2.5米/秒

因此B还要经历时间t₂才与C相撞：

 　 t₂==(1-0.25)/2.5=0.3秒，

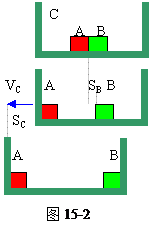
故C的位移为：S_C=V_Ct₂=1×0.3=0.3米，

方向向左，如图15-2所示。