Question

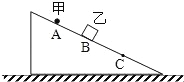
【题目】如图所示，在水平面的上方有一固定的水平运输带，在运输带的左端A处用一小段光滑的圆弧与一光滑的斜面平滑衔接，该运输带在电动机的带动下以恒定的向左的速度v0＝2 m/s运动．将一可以视为质点的质量为m＝2 kg的滑块由斜面上的O点无初速度释放，其经A点滑上运输带，经过一段时间滑块从运输带最右端的B点离开，落地点为C.已知O点与A点的高度差为H1＝1.65 m，A点与水平面的高度差为H2＝0.8 m，落地点C到B点的水平距离为x＝1.2 m，g取10 m/s2.

(1)求滑块运动到C点时的速度大小；

(2)如果仅将O点与A点的高度差变为H′1＝0.8 m，且当滑块刚好运动到A点时，撤走斜面，求滑块落在水平面上时的速度大小；

(3)在第(2)问情况下滑块在整个运动过程中因摩擦而产生的热量有多少？

Answer 1

【答案】(1)5 m/s (2)2 m/s (3)36 J

【解析】（1）设滑块滑至运输带的右端速度为v1，滑块自运输带右端飞出至落地时间为t，则在水平方向上 x=v1t
在竖直方向上 H2=gt2
设滑块落地时的速度为v，根据机械能守恒定律得
mv22+mgH2=mv2
由①②③解得 v1=3m/s，v=5m/s
（2）设滑块由H1=1.65m处由静止开始下滑到运输带，在滑到运输带右端过程中，摩擦力对滑块做功大小为Wf，由功能关系得
mgH1=mv12+Wf；
解得 Wf=24J
由于 mgH1′＜Wf，则滑块由H1′=0.8m处开始下滑到运输带，在滑到运输带右端前滑块的速度就应减为零，然后滑块要向左运动，设滑块由H1′=0.8m处静止开始下滑到运输带，在到达运输带左端的速度为v0′，则mgH1′=mv0′2
解得 v0′=4m/s
因为 v0＜v0′，故滑块向左运动的过程中，先加速至于运输带速度相同，后匀速运动至运输带左端作平抛运动，设滑块从运输带左端抛出落地时的速度大小为v2，根据机械能守恒定律得mv02+mgH2=mv22
解得 v2=2 m/s
（3）设滑块与运输带间的动摩擦因数为μ，滑块由H1′=0.8m处静止开始下滑到运输带，在运输带上滑到速度为零的过程中，滑块运动的时间为t1，滑块与运输带摩擦所产生的热量为Q1，则有
Q1=μmg（t1+v0t1）
又对滑块，由动能定理得

设滑块后来又向运输带左端运动的过程中，滑块加速至v0的时间为t2，滑块与运输带摩擦所产生的热量为Q2，则
Q2=μmg（v0t2+t2）
对滑块，由动能定理得

则滑块自释放至落地全过程中滑块与运输带摩擦所产生的热量 Q=Q1+Q2．
解得 Q=36J