题目内容
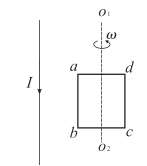
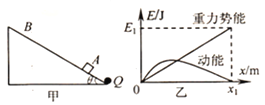
【题目】如图所示为一简化后的跳台滑雪的雪道示意图，运动员从O点由静止开始，在不借助其它外力的情况下，自由滑过一段圆心角为60°的光滑圆弧轨道后从A点水平飞出，然后落到斜坡上的B点。已知A点是斜坡的起点，光滑圆弧轨道半径为40m，斜坡与水平面的夹角θ＝30°，运动员的质量m＝50 kg，重力加速度g＝10 m／s2。下列说法正确的是
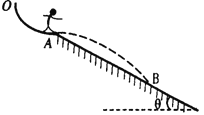
A. 运动员从O运动到B的整个过程中机械能守恒
B. 运动员到达A点时的速度为20 m／s
C. 运动员到达B点时的动能为10 kJ
D. 运动员从A点飞出到落到B点所用的时间为
s
【答案】AB
【解析】运动员在光滑的圆轨道上的运动和随后的平抛运动的过程中只受有重力做功，机械能守恒．故A正确；运动员在光滑的圆轨道上的运动的过程中机械能守恒，所以：
mvA2=mgh=mgR（1-cos60°）所以： 
，故B正确；设运动员做平抛运动的时间为t，则：x=vAt；y=
gt2
由几何关系： 
，联立得： 
， 
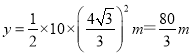
运动员从A到B的过程中机械能守恒，所以在B点的动能：EkB=mgy+
mvA2，代入数据得：EkB=
×105J．故C D错误．故选AB.
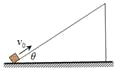
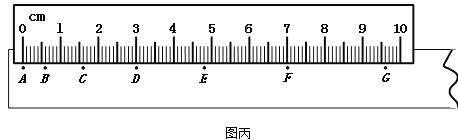
阅读快车系列答案
【题目】某同学利用如图所示的装置验证动能定理。该装置由斜面和很短一段水平部分组成，固定并调整斜槽，使它的末端O点的切线水平，在水平地面上依次铺放好木板、白纸、复写纸。将小球从不同的标记点由静止释放，记录小球到达斜槽底端时下落的高度H，并根据落点位置测量出小球平抛的水平位移x。
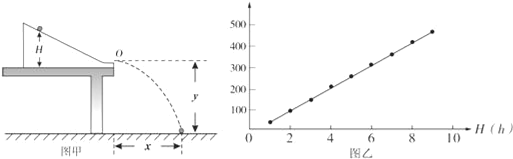
改变小球在斜槽上的释放位置，进行多次测量，记录数据如下：
高度H（h为单位长度） | h | 2 h | 3 h | 4 h | 5 h | 6 h | 7 h | 8 h | 9 h |
水平位移 x/cm | 5.5 | 9.1 | 11.7 | 14.2 | 15.9 | 17.6 | 19.0 | 20.6 | 21.7 |
（1）已知斜槽倾角为θ，小球与斜槽之间的动摩擦因数为μ，斜槽底端离地的高度为y。小球从斜槽上滑下的过程中，动能定理若成立应满足的关系式是（利用给定和测得的物理量）______。
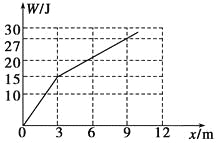
（2）以H为横坐标，以______为纵坐标，在坐标纸上描点作图，如图乙所示。图线不过坐标原点的原因是______。