题目内容
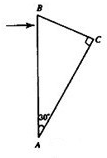 如图所示,某种透明物质制成的直角三棱镜ABC,∠A等于30°.一束光线在纸面内垂直AB边射入棱镜,如图所示,发现光线刚好不能从BC面射出,而是最后从AC面射出.求:
如图所示,某种透明物质制成的直角三棱镜ABC,∠A等于30°.一束光线在纸面内垂直AB边射入棱镜,如图所示,发现光线刚好不能从BC面射出,而是最后从AC面射出.求:①透明物质的折射率n.
②光线从AC面射出时的折射角α.(结果可以用α的三角函数表示)
分析:①光线从AB垂直射入,恰好在BC面发生全反射,根据几何关系求出临界角的大小,根据sinC=
求出透明物质的折射率.
②根据几何关系求出图中β的大小,然后通过折射定律求出折射角α的正弦值.
| 1 |
| n |
②根据几何关系求出图中β的大小,然后通过折射定律求出折射角α的正弦值.
解答: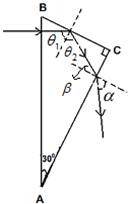 解:①由题意可知,光线从AB垂直射入,恰好在BC面发生全反射,光线最后从AC面射出,光路图如下图.
解:①由题意可知,光线从AB垂直射入,恰好在BC面发生全反射,光线最后从AC面射出,光路图如下图.
设该透明物质的临界角为C,由几何关系可知
C=θ1=θ2=60°,sinC=
解得:n=
②由几何关系知:β=30°
由折射定律n=
解得:sinα=
答:①透明物质的折射率n=
.
②光线从AC面射出时的折射角的正弦为
.
 解:①由题意可知,光线从AB垂直射入,恰好在BC面发生全反射,光线最后从AC面射出,光路图如下图.
解:①由题意可知,光线从AB垂直射入,恰好在BC面发生全反射,光线最后从AC面射出,光路图如下图.设该透明物质的临界角为C,由几何关系可知
C=θ1=θ2=60°,sinC=
| 1 |
| n |
解得:n=
2
| ||
| 3 |
②由几何关系知:β=30°
由折射定律n=
| sinα |
| sinβ |
解得:sinα=
| ||
| 3 |
答:①透明物质的折射率n=
2
| ||
| 3 |
②光线从AC面射出时的折射角的正弦为
| ||
| 3 |
点评:本题考查几何光学,关键掌握光的折射定律以及临界角与折射率的大小关系sinC=
.
| 1 |
| n |

练习册系列答案
相关题目
 (2011?泗阳县一模) (选做题)本题包括A、B、C三小题,请选定其中两题,并在相应答题区域内作答.若三题都做,则按A、B两题评分.
(2011?泗阳县一模) (选做题)本题包括A、B、C三小题,请选定其中两题,并在相应答题区域内作答.若三题都做,则按A、B两题评分.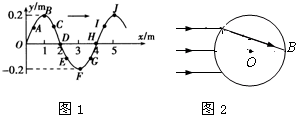 (3)图2示是一透明的圆柱体的横截面,其半径R=20cm,折射率为
(3)图2示是一透明的圆柱体的横截面,其半径R=20cm,折射率为 ,AB是一条直径,今有一束平行光沿AB方向射向圆柱体,试求:
,AB是一条直径,今有一束平行光沿AB方向射向圆柱体,试求:
