题目内容
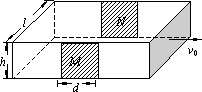
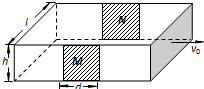
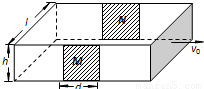
磁流体动力发电机的原理如图所示，一个水平放置的上下、前后封闭的横截面为矩形的塑料管，其宽度为l，高度为h，管内充满电阻率为ρ的某种导电流体(如水银)。矩形塑料管的两端接有涡轮机，由涡轮机提供动力使流体通过管道时具有恒定的水平向右的流速v0。管道的前、后两个侧面上各有长为d的相互平行且正对的铜板M和N。实际流体的运动非常复杂，为简化起见作如下假设：①垂直流动方向横截面上各处流体的速度相同；②流体不可压缩。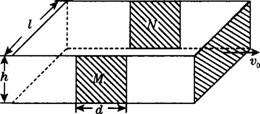
(1)若在两个铜板M、N之间的区域加有竖直向上、磁感应强度为B的匀强磁场，则当流体以稳定的速度v0流过时，两铜板M、N之间将产生电势差。求此电势差的大小，并判断M、N两板哪个电势较高；
(2)用电阻可忽略不计的导线将铜板M、N外侧相连接，由于此时磁场对流体有力的作用，使流体的稳定流速变为v(v＜v0)，求磁场对流体的作用力；
(3)为使流体的流速增加到原来的值v0，涡轮机提供动力的功率必须增加，假设流体在流动过程中所受的阻力与它的流速成正比，试推导出新增加功率的表达式。
(1)由法拉第电磁感应定律，两铜板间的电势差U=E=Blv0
由右手定则可判断出M板的电势较高
(2)用电阻可忽略不计的导线将铜板M、N外侧相连接，即铜板由外侧短路后，M、N两板间的电动势E=Blv
短路电流I=E／R内 R内=ρ
磁场对流体的作用力F=BIl
解得：F=
方向与v方向相反(或水平向左)
(3)设流体在流动过程中所受‘的阻力与流速的比例系数为k，所以在外电路未短路时流体以稳定速度v0流过，此时流体所受的阻力(即涡轮机所提供的动力)
F0=kv0
此时涡轮机提供的功率P0=F0v0=k
外电路短路后，流体仍以稳定速度v0流过时，设此时磁场对流体的作用力为F磁，根据第(2)问的结果可知
F磁=
此时涡轮机提供的动力F1=F0+F磁=kv0+
此时涡轮机提供的功率Pt=Ftv0=k
+
所以新增加功率△P=P1-P0=
。
说明：第(3)问如果采用如下做法也得6分：
外电路没有接通，流体以稳定速度v0流过时，磁场对流体无作用力；外电路短路后，流体仍以稳定速度v0流过，设此时磁场对流体的作用力为F磁，外接涡轮机必须增加压力F用以平衡F磁，即F=F磁
根据第(2)问的结果可知F磁=
此时涡轮机新增加的功率△P=Fv0=
互动英语系列答案
名牌学校分层周周测系列答案
（2007?海淀区模拟）磁流体动力发电机的原理如图所示，一个水平放置的上下、前后封闭的横截面为矩形的塑料管，其宽度为l，高度为h，管内充满电阻率为ρ的某种导电流体（如水银）．矩形塑料管的两端接有涡轮机，由涡轮机提供动力使流体通过管道时具有恒定的水平向右的流速v0．管道的前、后两个侧面上各有长为d的相互平行且正对的铜板M和N．实际流体的运动非常复杂，为简化起见作如下假设：①垂直流动方向横截面上各处流体的速度相同；②流体不可压缩；③当N、N之间有电流通过时，电流只从M、N之间正对的区域内通过．
