��Ŀ����
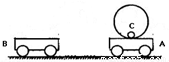
 �⻬ˮƽ���Ϸ�������С��A��B��A���Ϲ̶�һ������ҲΪm���ڱڹ⻬��Ӳ��ԲͲ��Ͳ����һ����Ϊ2m�Ĺ⻬С��C��C�������Ϊ�ʵ㣩��C��λ��ԲͲ��͵�B��������Ϊ4m������С��A��С��C��Ծ�ֹ��������V0�����˶���С��B��V0���������˶���ijʱ��������������������������������ʱ�伫�̣���B����ֹ��A����ԭ����V0��������
�⻬ˮƽ���Ϸ�������С��A��B��A���Ϲ̶�һ������ҲΪm���ڱڹ⻬��Ӳ��ԲͲ��Ͳ����һ����Ϊ2m�Ĺ⻬С��C��C�������Ϊ�ʵ㣩��C��λ��ԲͲ��͵�B��������Ϊ4m������С��A��С��C��Ծ�ֹ��������V0�����˶���С��B��V0���������˶���ijʱ��������������������������������ʱ�伫�̣���B����ֹ��A����ԭ����V0����������1��A����������С��
��2��A����������֪С����������ߵ����Ͳ�����ģ���A���ܻ�õ����������ٶȵĴ�С��
��������1��A��B��ײ�����У�A��B��ɵ�ϵͳ�����غ㣬���ݶ����غ㶨�����A��������
��2��A��������С����������ߵ㴦���ٴη�����͵������˶�ʱ����A�������������ٶȣ���A��C�Ķ����غ㶨�ɼ���е���غ㼴����⣮
��2��A��������С����������ߵ㴦���ٴη�����͵������˶�ʱ����A�������������ٶȣ���A��C�Ķ����غ㶨�ɼ���е���غ㼴����⣮
����⣺��1��A��B������ȡ����Ϊ�������ɶ����غ��
4mv0+��m+mA����-v0��=��m+mA��v0
��� mA=m
��2��A��������С����������ߵ㴦���ٴη�����͵������˶�ʱ����A�������������ٶȣ����ٶȴ�СΪvA��C���ٶȴ�СΪvc�����A��CԲͲ��ɵ�ϵͳ�����㶯���غ�ͻ�е���غ㣬��
��mA+m��v0+2m��-v0��=��mA+m����-vA��+2mvc
(mA+m)
+
2m
=
(mA+m)
+
2m
��� vA=vc=v0
��A���ܻ�õ���������ٶȴ�СΪv0��
��
��1��A������������m��
��2��A����������֪С����������ߵ����Ͳ�����ģ�A���ܻ�õ����������ٶȵĴ�СΪv0��
4mv0+��m+mA����-v0��=��m+mA��v0
��� mA=m
��2��A��������С����������ߵ㴦���ٴη�����͵������˶�ʱ����A�������������ٶȣ����ٶȴ�СΪvA��C���ٶȴ�СΪvc�����A��CԲͲ��ɵ�ϵͳ�����㶯���غ�ͻ�е���غ㣬��
��mA+m��v0+2m��-v0��=��mA+m����-vA��+2mvc
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 c |
��� vA=vc=v0
��A���ܻ�õ���������ٶȴ�СΪv0��
��
��1��A������������m��
��2��A����������֪С����������ߵ����Ͳ�����ģ�A���ܻ�õ����������ٶȵĴ�СΪv0��
������������Ҫ�����˶����غ㶨�ɼ������غ㶨�ɵ�ֱ��Ӧ�ã��ؼ����ж�A���ܻ����������ٶȵ�������

��ϰ��ϵ�д�
 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
�����Ŀ
 ������ѡ��3-5ģ�顿
������ѡ��3-5ģ�顿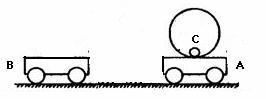
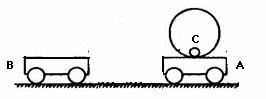 A����������С����Ͳ�������������߶ȣ���֪С����������ߵ����Ͳ�����ģ�
A����������С����Ͳ�������������߶ȣ���֪С����������ߵ����Ͳ�����ģ�