题目内容
.如图甲所示,一长绝缘木板靠在光滑竖直墙面上,质量为m=1kg.木板右下方有一质量为2m的小滑块(可视为质点),滑块与木板间的动摩擦因数为μ=0.4,木板与滑块处有恒定的风力F=4mg,风力方向水平向左,若电动机通过一根绝缘绳拉动滑块(绳保持竖直),使之从地面由静止开始匀加速向上移动,当滑块与木板分离时(如图乙所示),滑块的速度大小为v=8m/s,此过程中电动机对滑块做的功为W0=136J(重力加速度为g=10m/s2).
(1)求当滑块与木板分离时,滑块离地面的高度h;
(2)滑块与木板分离前,木板运动的加速度大小a;
(3)求滑块开始运动到与木板分离的过程中摩擦力对木板所做的功W.
(1)2m(2)6m/s2(3)12J
解析试题分析:(1) 滑块与木板间的正压力大小为:FN=F=4mg ①
滑块与木板间的摩擦力大小: Ff=μFN ②
滑块向上运动过程由动能定理得: W0-2mgh-Ffh= ×2mv2 ③
×2mv2 ③
联立①②③三式,代入数据得:h=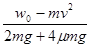 =2m
=2m
(2)对长木板由牛顿第二定律得:Ff-mg=ma ④
联立④⑤代入数据得: a = 6m/s2
(3)摩擦力对木板做功为 W=Ff S ⑤
S=at2 ⑥
又:h=vt/2 ⑦
由以上各式解得:W=12J
考点:此题考查了牛顿定律及动能定理。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
关于两个物体间的作用力和反作用力,下列说法中正确的是( )
| A.作用力和反作用力可以是不同性质的 |
| B.作用力和反作用力可以不同时产生 |
| C.作用力和反作用力的效果会相互抵消 |
| D.作用力和反作用力一定同时产生,同时消失 |
 时,装置可安全工作。 一质量为m 的小车若以速度
时,装置可安全工作。 一质量为m 的小车若以速度 撞击弹簧,可使轻杆向右移动了
撞击弹簧,可使轻杆向右移动了 。轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦。
。轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦。